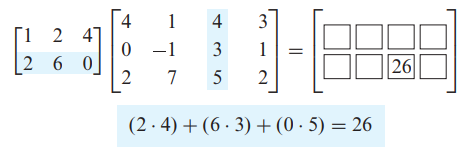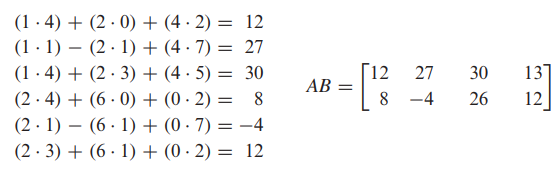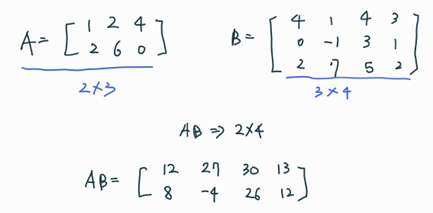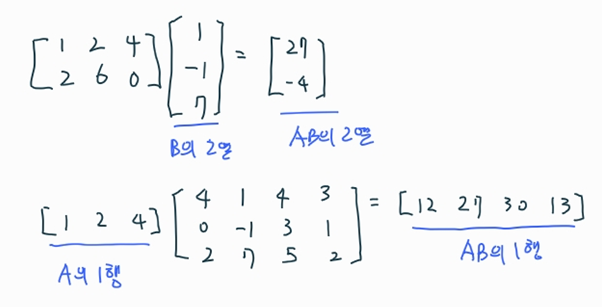목차
Elementary Linear Algebra [Anton]을 참고하여 작성하였습니다.
행렬의 표기법과 용어
- 행렬은 숫자들의 직사각형 배열입니다. 배열 안에 있는 숫자들은 행렬의 원소라고 합니다.
- 벡터는 보통 굵은 소문자를 사용해서 표현합니다.
- 행렬에서 m과 n이 같은 경우 정방행렬(square matrix)라고 합니다. 정방행렬의 대각선의 값은 행렬의 주대각선(main diagonal)이라고 합니다.
행렬의 연산
- 행렬의 덧셈과 뺄셈은 행렬의 크기가 같을 때만 가능합니다.
- 행렬의 스칼라곱은 각 원소에 스칼라값을 곱해주면 됩니다.
- 행렬의 곱셈은 앞의 행렬의 column의 개수와, 뒤 행렬의 row 개수가 같아야지만 연산이 가능합니다.
- AB의 i행 j열 값은 A의 i 행 x B의 j열 연산을 통해 값을 얻어낼 수 있습니다.
- [행렬 곱셈의 예시]
분할된 행렬(Partitioned Matrices)
- 행렬은 선택된 행과 열 사이에 수평선과 수직선을 넣어서 더 작은 행렬로 분할될 수 있습니다.
열벡터와 행벡터에 의한 행렬 곱셈
- 분할은 많은 곳에서 사용되는데 이 중에 하나는 행렬의 곱 AB의 특정한 행이나 열을 전체를 다 계산하지 않고 찾아내는 것입니다. AB의 각 열벡터는 B를 열벡터로 분할해 곱하여 얻을 수 있고, AB의 각 행벡터는 A를 행벡터로 분할해 곱하여 얻을 수 있습니다.
- 만약 AB 연산결과에서 2번째 열만 필요하다면 AB를 전체를 계산할 필요 없이 B의 2열만을 이용하여 계산할 수 있습니다. 마찬가지로 1번째 행만 필요하다면 AB를 전체를 계산하지말고 A의 1행만을 이용하여 계산할 수 있습니다.
[참고] 일차결합(linear combination)으로의 행렬 곱셈
- 행렬 곱셈의 또 다른 방법입니다. (참고용으로 알아두기. 기본적으로는 기본 행렬 곱셈 방식을 많이 사용)
- 만약에 A1,A2,..., Ar이 같은 크기의 행렬이고, c1, c2,..., cr이 스칼라이면 c1A1 + c2A2 + ... + crAr은 계수가 c1, c2,..., cr인 A1, A2,..., Ar의 일차결합(linear combination)이라고 합니다.
- 이것을 생각해서 Ax를 일차결합으로 표현해보겠습니다. 계수가 x벡터의 원소들인, A의 열벡터들의 일차결합이 됩니다.

- [예시 1]
- [예시 2]
연립일차방정식의 행렬 형태
- 연립일차방정식을 행렬로 표현하면 다음과 같습니다.

- 여기서 A는 계수행렬(coefficient matrix)이고 첨가행렬까지 되려면 b 벡터까지 첨가되어야지 첨가행렬(augmented matrix)이 됩니다.

전치행렬(Transpose)
- A가 m x n 행렬이면 A의 전치행렬(A^(T))은 n x m 행렬이고 A의 행과 열을 바꾼 행렬입니다.

- 둘 이상에 대해서도 동일하게 적용됩니다.
- (ABC)^(T) = C^(T)B^(T)A^(T)
- 둘 이상에 대해서도 동일하게 적용됩니다.
행렬의 대각합(trace)
- A가 정방행렬이라면 A의 대각합(trace)은 tr(A)로 표기되고 A의 주 대각선 상에 있는 원소들의 합으로 정의가 됩니다. 만약 A가 정방행렬이 아니면 A의 대각합은 정의되지 않습니다.
'Math > 선형대수' 카테고리의 다른 글
| 6. 연립일차방정식과 역행렬에 관한 여러 가지 결과 (1) | 2023.11.27 |
|---|---|
| 5. 기본행렬(Elementary Matrix) (0) | 2023.11.27 |
| 4. 행렬의 대수적 성질 / 역행렬 (1) | 2023.11.27 |
| 2. 가우스 소거법 (1) | 2023.11.26 |
| 1. 연립일차방정식의 소개 (0) | 2023.11.26 |