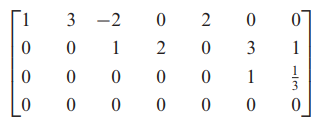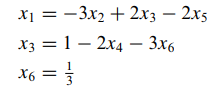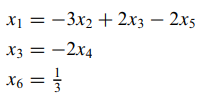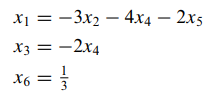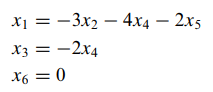목차
Elementary Linear Algebra [Anton]을 참고하여 작성하였습니다.
사다리꼴(Echelon Forms)
- 연립일차방정식의 소개에서 연립일차방정식에 대한 첨가행렬을 간단히 하여 해 x=1, y=2, z=3을 얻었습니다. 이 행렬은 기약 행사다리꼴(reduced row echelon form)입니다.
- 기약 행사다리꼴(reduced row echelon form) 형태를 가지기 위해서는 다음 4가지 성질을 가져야 합니다.
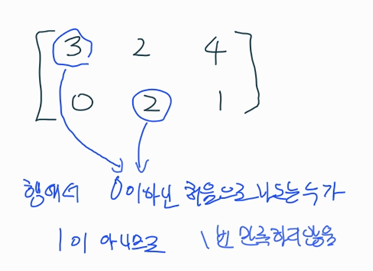
- 0이 아닌 원소를 갖는 행에서 맨 처음 나오는 0이 아닌 수는 1이어야 합니다. (이것을 선도 1(leading 1)이라고 합니다.)
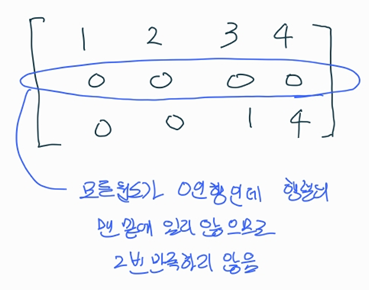
- 모든 원소가 0인 행이 있다면 그 행은 행렬의 맨 밑으로 내려가야 합니다.
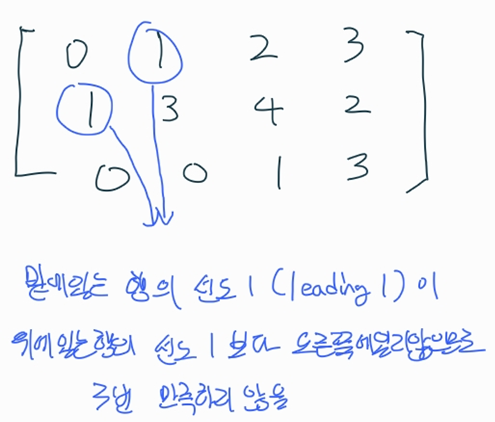
- 영이 아닌 원소를 갖는 연속된 두 행은 밑에 있는 행의 선도 1이 위에 있는 행의 선도 1보다 오른쪽에 있어야 합니다.
- 선도 1이 있는 열의 나머지 원소들은 모두 0이어야 합니다.
- 0이 아닌 원소를 갖는 행에서 맨 처음 나오는 0이 아닌 수는 1이어야 합니다. (이것을 선도 1(leading 1)이라고 합니다.)
- 여기서 1, 2, 3번을 만족한다면 행사다리꼴(row echelon form)이고, 1,2,3,4번 모두를 만족한다면 기약 행사다리꼴(reduced row echelon form)이 됩니다.
- 모든 행렬은 유일한 기약 행사다리꼴을 갖지만, 행사다리꼴은 유일하게 갖지 않습니다. 기본 행연산의 순서가 다르면 다른 행사다리꼴이 나오게 됩니다.
- 행사다리꼴과 기약 행사다리꼴의 예시를 살펴보겠습니다.
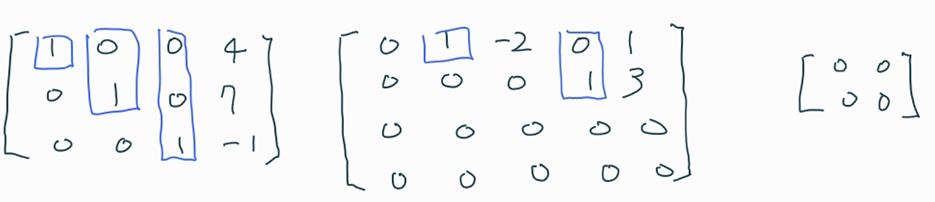
- [행사다리꼴의 예시]
- [기약 행사다리꼴의 예시]
- [행사다리꼴의 예시]
기약 행사다리꼴을 통해 해를 찾는 과정
- 그럼 이제 어떤 연립방정식의 첨가행렬을 기본 행 연산을 통해 기약 행사다리꼴로 만들고 해를 찾는 과정을 살펴보도록 하겠습니다.
- 다음과 같은 미지수 x,y,z에 대한 연립방정식의 첨가행렬이 기본 행 연산을 통해 다음과 같은 기약 행사다리꼴이 되었다고 가정할 때 각각의 해를 구해보겠습니다.

- (a)의 경우 첨가행렬의 마지막 행이 0x+0y+0z=1로 어떠한 x, y, z에 대해서도 성립하지 않습니다. 이처럼 0 0 0 ,... , 0, 0, x 같이 마지막만 값이 있는 경우의 행을 peculiar row라고 합니다. 즉, peculiar row가 존재하는 경우는 해가 없습니다.
- (b)의 경우 첨가행렬의 마지막 행이 0x+0y+0z=0으로 생략이 가능합니다. 따라서 두 개의 식으로 표현되는데, 이때 선도 1에 해당하는 변숫값들(여기선 x와 y)은 선도변수(leading variable)이라고 하고, 나머지 변수(여기선 z)들은 자유변수(free variable)이라고 합니다. 여기선 자유변수가 1개 있기 때문에 일반해는 직선의 형태를 가지게 됩니다. (자유변수 z를 매개변수로 취급하여 임의의 값 t로 설정하여 x와 y를 구할 수 있습니다.)
- x=-1-3t / y=2+4t / z=t
- (c)의 경우는 첨가행렬 중 0 0 0 0이 2개가 존재하여, x-5y+z=4식만 남게되는데 이때 선도 1에 해당하는 x를 제외하고는 모두 자유변수가 됩니다. 자유변수가 2개이기 때문에 일반해는 평면의 형태를 가지게 됩니다.
- x=4+5s-t / y=s / z=t
- 참고 : 일반해(general solution)의 정의
- 연립일차방정식이 무수히 많은 해를 가질 때, 매개변수에 숫자를 넣어 해를 얻을 수 있는 매개변수 방정식들의 집합을 그 연립방정식의 일반해(general solution)라고 합니다.
(자유변수가 없을경우는 일반해는 특정한 하나의 해를 가지개 됩니다.)
- 연립일차방정식이 무수히 많은 해를 가질 때, 매개변수에 숫자를 넣어 해를 얻을 수 있는 매개변수 방정식들의 집합을 그 연립방정식의 일반해(general solution)라고 합니다.
가우스-요르단(Gauss-Jordan) 소거법
- 연립일차방정식의 해를 구할 때 그것의 첨가행렬로부터 기약 행사다리꼴을 구하면 쉽게 해를 구할 수 있는 것을 확인했었습니다. 그럼 이제 임의의 행렬을 기약 행사다리꼴로 만들기 위한 소거법(elimination)을 단계별로 살펴보겠습니다.
- (1. 연립일차방정식의 소개에서 했던 첨가행렬의 기본 행연산과 유사합니다.)

- 풀이 과정
- [1단계] 0이 아닌 원소가 있는 가장 왼쪽의 열에서 계산을 시작합니다.
- [2단계] 필요하다면, 1단계에서 찾은 열의 가장 윗수가 영이 아니도록 첫째 행과 다른 행을 바꿉니다.
- [3단계] 1단계에서 찾은 열의 가장 윗수가 a이면 1/a를 곱하여 1로 바꿉니다.
- [4단계] 1행에 적당한 수를 곱하여 아래 행들에게 더하여 선도 1의 아래 원소들이 모두 0이 되도록 합니다.
- [5단계] 행렬의 1행은 두고 나머지 부분행렬에 대해서 다시 1단계부터 진행하여 행사다리 꼴이 될 때까지 반복합니다.
- [6단계] 모든 행에 대해서 진행을 완료하면 행사다리꼴 행렬이 됩니다. 추가적으로 기약 행사다리꼴이 되기 위해서는 마지막 0이 아닌 행부터 시작하여 위로 올라가면서 선도 1의 위를 0으로 만들기 위한 적당한수를 곱하여 위의 행에 더해줍니다.
- (여기서 선도 1 아랫부분을 모두 0으로 하는 것을 전진(forward) 단계(1~5단계), 선도 1 윗부분을 모두 0으로 하는 것을 후진(backward) 단계(6단계)라고 합니다. 만약 forward 단계만 진행한다면 기약 행사다리꼴이 아닌 행사다리꼴이 만들어지는데 이렇게 forward단계만 진행하면 가우스 요르단 소거법이 아닌 가우스 소거법이라고 합니다.)
- [1단계] 0이 아닌 원소가 있는 가장 왼쪽의 열에서 계산을 시작합니다.
가우스 소거법과 역대입법(back-substitution)
- 손으로 풀 수 있는 작은 연립방정식들의 경우는 기약 행사다리꼴을 찾는 가우스-요르단 소거법을 사용하는 것이 좋습니다. 하지만 컴퓨터로 해를 찾아야 하는 큰 연립방정식의 경우는 일반적으로 가우스 소거법으로 행사다리꼴을 만든 뒤 역대입법(back-substitution)이라고 불리는 과정을 이용하여 완결하는 것이 낫습니다.
- 다음 연립방정식을 가우스 소거법과 역대입법을 이용하여 풀어보며 이해해 보도록 하겠습니다.
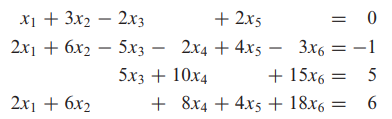
- 먼저 가우스 소거법(forward 과정)을 통한 첨가행렬의 행사다리꼴은 다음과 같습니다.
- 역대입법은 다음과 같습니다.
- [1단계] 선도변수에 대하여 방정식을 풉니다.
- [2단계] 밑의 방정식부터 시작하여, 연속적으로 각 방정식을 위의 방정식에 대입하여 위로 갑니다.
- 먼저 x6을 두 번째 방정식에 대입합니다. (첫 번째 방정식까지도 원래는 대입해야하지만 첫 번째 방정식은 x6에 관한 값이 없으므로 pass 된 것입니다.)
- 다음으로 두번째 방정식을 첫 번째 방정식에 대입하여 다음값을 얻습니다.
- 먼저 x6을 두 번째 방정식에 대입합니다. (첫 번째 방정식까지도 원래는 대입해야하지만 첫 번째 방정식은 x6에 관한 값이 없으므로 pass 된 것입니다.)
- [3단계] 남은 자유변수에(만약 존재한다면) 임의의 값을 대입하면 일반해가 구해집니다.
- [1단계] 선도변수에 대하여 방정식을 풉니다.
- [가우스 소거법 + 역대입법]은 가우스-요르단 소거법과 비슷하지만, backward 단계가 없고 밑에 방정식부터 위의 방정식들에 대입하는 방식으로 바꾼 방법입니다.
동차(homogeneous) 연립일차방정식
- 상수항이 모두 0이면 이를 동차 연립일차방정식이라고 합니다. 이럴 경우는 모든 연립방정식이 x1=0, x2=0, ... , xn=0을 해로 갖습니다. 이 해를 자명해(trivial solution)라고 합니다.
- 동차 연립일차방정식은 늘 자명해를 갖기 때문에 해에 대해서는 '자명해만 있다' 또는 '자명해 외에 무수히 많은 해가 있다(비자명해(nontrivial solution)가 존재하는 경우)' 이 두 가지 가능성밖에 없습니다. (즉, 해가 없는 경우가 없음. peculiar row가 존재할 가능성이 없기 때문)
-

- 미지수가 2개인 경우를 예시를 들어보면 다음과 같습니다.
-
- 동차 연립방정식이 항상 비자명해를 갖는 경우가 있는데 이는 방정식보다 미지수의 개수가 더 많은 경우입니다.
- 예를 들어 미지수는 6개인데 방정식이 4개인 경우를 살펴보겠습니다.

- 위 동차 연립방정식을 기약 행사다리꼴로 나타내면 다음과 같습니다. 즉 선도변수는 x1, x3, x6이며 나머지는 자유변수가 됩니다.

- 선도변수에 대해서 정리하면 다음과 같이 나오게 됩니다.
- 따라서 x2, x4, x5에 따라 해가 달라지기 때문에 이럴 경우는 항상 비자명해를 가지게 됩니다. 즉, 동차 연립방정식인데 선도변수에 의해 정리했을 경우 자유변수가 존재한다면 항상 비자명해가 존재하게 됩니다. (자명해는 x2 = x4 = x5 = 0일 때이고, 이외의 모든 경우는 비자명해입니다.)
- 이와 같은 과정을 통해 알 수 있는 점은 동차연립일차방정식이 n개의 미지수를 갖고, 그것의 첨가행렬의 기약 행사다리꼴이 r개의 0이 아닌 행을 갖는다면, 이 연립방정식은 n-r개의 자유변수를 갖게 됩니다. 즉 n-r>=1일 경우 비자명해가 반드시 존재합니다. (= 동차 연립일차방정식에서 (n-r>=1) 일 경우 무수히 많은 해를 갖습니다.)
- 예를 들어 미지수는 6개인데 방정식이 4개인 경우를 살펴보겠습니다.
- 동차 연립일차방정식은 동차기 때문에 항상 마지막 열은 행연산을 하더라도 동차(0, 0,..., 0)를 계속해서 유지하므로 peculair row가 존재하는 경우는 절대 없습니다. 따라서 무수히 많은 해를 갖거나 자명해만 갖거나 이 두 가지 경우밖에 존재하지 않습니다. (단, 동차가 아닐 경우는 peculiar row가 존재할 가능성이 있기 때문에 해가 없는 경우도 존재합니다.)
'Math > 선형대수' 카테고리의 다른 글
| 6. 연립일차방정식과 역행렬에 관한 여러 가지 결과 (1) | 2023.11.27 |
|---|---|
| 5. 기본행렬(Elementary Matrix) (0) | 2023.11.27 |
| 4. 행렬의 대수적 성질 / 역행렬 (1) | 2023.11.27 |
| 3. 행렬과 행렬 연산 (4) | 2023.11.27 |
| 1. 연립일차방정식의 소개 (0) | 2023.11.26 |