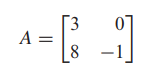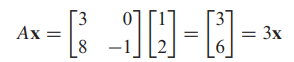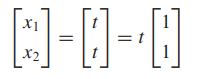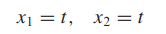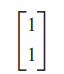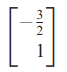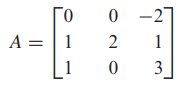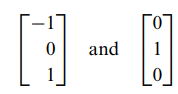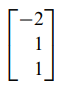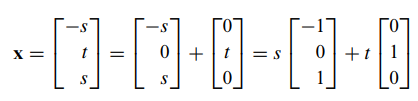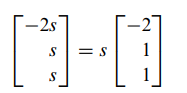목차
Elementary Linear Algebra [Anton]을 참고하여 작성하였습니다.
고유값(eigenvalue)과 고유벡터(eigenvector)의 정의
- 정의
- A가 n x n 행렬일 때, R^n에 속하는 영이 아닌 벡터 x에 대해서 Ax가 x의 스칼라배이면(즉, 어떤 스칼라 λ에 대해서 Ax= λx이면) x를 A의 고유벡터(eigenvector)라 합니다. 그리고 스칼라 λ를 A의 고유값(eigenvalue)이라 하며 x를 λ에 대응하는 고유벡터(eigenvector corresponding to λ)라 합니다.
- 정의만 보면 이해가 안될수가 있습니다. 간략하게 설명하면 다음과 같습니다.
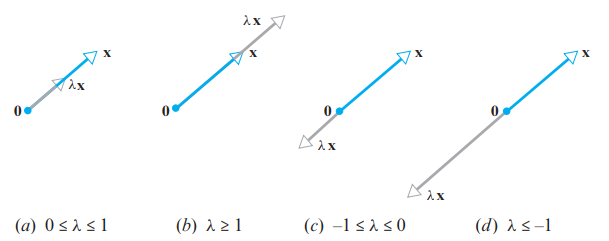
- 일반적으로 벡터 x에 정방행렬 A를 곱하게 되면 벡터 x의 크기와 방향은 다르게 됩니다. 하지만 x가 A의 고유벡터인 경우에는 A의 곱에 의해 방향이 바뀌지 않게 됩니다.
- 즉, A의 곱에 의해서 방향이 변하지 않는 벡터를 고유벡터(eigenvector)라고 합니다.
- 하지만 λ가 음인 경우 방향을 반대로 향하게 됩니다.
- 또한, 그 변한 크기를 λ, 즉 고유값(eigenvalue)라고 합니다.
- 2 x 2 행렬의 고유 벡터 예시를 살펴보도록 하겠습니다.
- 행렬 A
- 벡터 x = [1,2]는 행렬 A의 고유벡터(eigenvector)입니다.(고유값(eigenvalue)은 3)
- 행렬 A
고유값과 고유벡터의 계산 (참고 : 고유공간(eigenspace))
- 그렇다면 n x n 행렬 A의 고유값과 고유벡터를 어떻게 찾을 수 있을까요?
- 먼저 A에 대한 고유값을 찾습니다.
- Ax= λx는 Ax=λIx로 다시 쓸수 있습니다. 이를 정리하면 다음과 같이 표현됩니다.
- (λI - A)x = 0
- λ가 A의 고유값이기 위해서는 이 방정식의 영이 아닌 해 x가 존재해야 합니다. 따라서 다음 조건을 만족해야 합니다.
- det( λI - A) = 0
- 0이 아니라면 역행렬이 존재해서 x는 0이 되어버립니다.
- 이 식을 A의 특성방정식(characteristic equation)이라 합니다.
- det( λI - A) = 0
- Ax= λx는 Ax=λIx로 다시 쓸수 있습니다. 이를 정리하면 다음과 같이 표현됩니다.
- 다음으로 가능한 고유값들을 찾으면 그 값들을 아래 식에 대입합니다. 대입된 식에서 x가 비자명해가 되는 고유벡터를 찾으면 고유값과 고유벡터를 찾을 수 있습니다.
- (λI - A)x = 0
- 먼저 A에 대한 고유값을 찾습니다.
- [예제] 2x2 행렬의 고유값 찾기
- 행렬 A
- 행렬 A의 모든 고유값을 찾기 위해 특성방정식을 계산합니다.
- det( λI - A) = 0
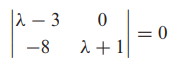
- ( λ-3)( λ+1)=0
- 따라서 행렬 A는 3과 -1을 고유값 후보로 가질 수 있습니다.
- 행렬 A
- [예제] 3x3 행렬의 고유값
- 행렬 A
- 특성방정식 계산
- det( λI - A) = 0

- λ( λ( λ-8)+17 ) + (-4)(1) = λ^3 - 8λ^2 + 17λ -4
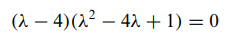

- 행렬 A
- 상삼각행렬 / 하삼각행렬 의 고유값
- 상삼각행렬 (하삼각행렬도 동일하게 적용)
- 특성방정식


 가 됩니다.
가 됩니다.
- 이처럼 상삼각행렬이나 하삼각행렬의 경우 고유값은 행렬의 대각성분이 됩니다.
- 상삼각행렬 (하삼각행렬도 동일하게 적용)
- 고유공간(eigenspace)이란?
- 먼저 고유벡터의 정확한 정의먼저 살펴보도록 하겠습니다.
- 고유벡터란 고유값을 구하고 고유값을 (λI - A)x = 0 식에 대입했을때 행렬 λI - A 의 영공간에 속하는 영이 아닌 벡터를 고유벡터라고 합니다.
- 영공간이란?
- 행렬 A의 영공간(null space)란 행렬 A에 의해 생성된 선형 변환의 결과가 영벡터인 모든 벡터의 집합입니다.
- 다시 말해서, 행렬 의 영공간은 모든 벡터 에 대해 다음을 만족하는 벡터들의 집합입니다.
- Av=0
- 여기서 는 영벡터(모든 성분이 0인 벡터)입니다.
- 영공간이란?
- 고유벡터란 고유값을 구하고 고유값을 (λI - A)x = 0 식에 대입했을때 행렬 λI - A 의 영공간에 속하는 영이 아닌 벡터를 고유벡터라고 합니다.
- 고유벡터의 정의에서 λ에 대응하는 A의 영공간(= (λI - A)의 영공간)을 고유공간(eigenspace)이라고 합니다.
- 먼저 고유벡터의 정확한 정의먼저 살펴보도록 하겠습니다.
- [예제] 고유공간의 기저(Bases for Eigenspaces)
- 행렬 A
- 특성방정식
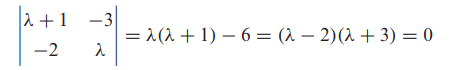
- 따라서 행렬 A의 고유값들은 2와 -3인 것을 알 수 있습니다. 고유값이 2개가 존재하므로 고유공간도 2개가 존재합니다.
- x가 비자명해를 가지는 (λI - A)x = 0 식을 구하기
- 고유값이 2일 경우
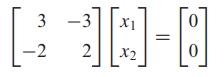
- 고유벡터
- 고유공간에 대한 기저(basis)
- 고유값이 -3일경우
- 같은 방식으로 계산해보면 고유공간에 대한 기저는 다음과 같습니다.
- 같은 방식으로 계산해보면 고유공간에 대한 기저는 다음과 같습니다.
- 고유값이 2일 경우
- 참고
- 행렬 A
- [예제] 고유공간의 고유벡터와 기저
- 행렬 A
- 특성방정식
- det(λI-A)=0
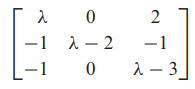
- λ(( λ-2)( λ-3))+2(λ-2) = λ^3 - 5λ^2 + 8λ -4 =0
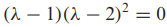
- det(λI-A)=0
- x가 비자명해를 가지는 (λI - A)x = 0 식을 구하기
- 고유값 2일때
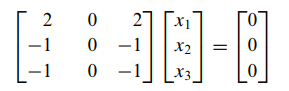
- 가우스 소거법을 사용하면 다음과 같이 나오게 됩니다.
- x1+x3 = 0
- 따라서 x1 = -s , x2 = t , x3 = s가 됩니다.
- 그러므로 고유벡터는 다음과 같이 표현됩니다.
- 이에 따른 기저(basis)
- 고유값 1일때
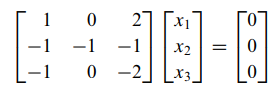
- 가우스 소거법
- x1+2(x3) = 0 // x2-x3 = 0
- 따라서 x1 = -2s, x2 = s, x3 = s 가 됩니다.
- 고유벡터
- 기저
- 고유값 2일때
- 행렬 A
행렬 A^n(power)에 대한 고유값과 고유벡터
- 행렬 A의 고유값과 고유벡터가 구해진다면 A의 임의의 양의 정수의 거듭제곱에 관한 고유값과 고유벡터는 간단히 구해질 수 있습니다.

- 고유값은 행렬의 제곱만큼 동일하게 제곱되지만, 고유벡터는 그대로 유지됩니다.
- [예제] 행렬의 거듭제곱의 고유값과 고유벡터
- 행렬 A
- 행렬 A의 고유값과 고유벡터는 위에서 계산했듯이 다음과 같습니다.
- 고유값
- λ = 1 and λ = 2
- 고유벡터
- λ = 2
- λ = 1
- λ = 2
- 고유값
- 그렇다면 A^7 에 대한 고유값과 고유벡터는 어떻게 될까요?
- 고유값
- λ = 2^7 = 128
- λ = 1^7 = 1
- 고유벡터
- 고유벡터는 그대로 유지
- 고유값
- 행렬 A
'Math > 선형대수' 카테고리의 다른 글
| 12. n차원에서의 놈(Norm), 거리(Distance), 점곱(Dot Product) (1) | 2023.11.30 |
|---|---|
| 11. 2차원, 3차원, n차원 공간에서의 벡터 (1) | 2023.11.28 |
| 10. 행렬식의 성질 / 크라머의 규칙 (1) | 2023.11.28 |
| 9. 행축소에 의한 행렬식 계산 (1) | 2023.11.28 |
| 8. 여인수 전개에 의한 행렬식(determinant) (0) | 2023.11.28 |