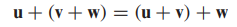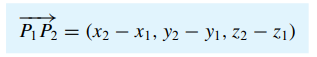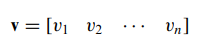목차
Elementary Linear Algebra [Anton]을 참고하여 작성하였습니다.
기하적 벡터
- 2차원 공간(2-공간) 또는 3차원 공간(3-공간)에서의 벡터를 화살표로 표시합니다.
- 화살표의 방향이 벡터의 방향을, 화살표의 길이가 벡터의 크기(magnitude)를 나타냅니다.
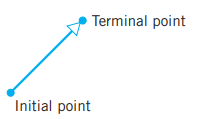
- 화살표의 시작 부분을 벡터의 시점(initial point), 그리고 끝부분을 벡터의 종점(terminal point)라고 부릅니다.
- A가 시점, B가 종점으로 하는 벡터는 다음과 같이 표시합니다.
- 벡터는 굵은 소문자로 나타내고 스칼라는 그냥 소문자로 나타냅니다.
- 벡터 :
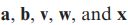
- 스칼라 :

- 벡터 :
- 아래 그림처럼 길이와 방향이 같은 벡터들은 동등(equivalent)하다고 합니다.

- 벡터는 단지 길이와 방향에 의해서만 결정되기 때문에 벡터들이 다른 위치에 있더라도 길이와 방향만 같다면 같은 벡터로 간주합니다.
- 시점과 종점이 같은 벡터는 영벡터(zero vector)라고 부릅니다.
 기호로 표시
기호로 표시- 영벡터의 경우 주어진 방향이 없기 때문에 문제에 따라 방향을 정하여 사용할 수 있습니다.
벡터 덧셈(Vector Addition)
- v + w 는 w에 의한 v의 평행이동 또는 v에 의한 w의 평행이동이라고 합니다.


- 평행사변형의 대각선이 합을 의미하게 됩니다.
벡터 뺄셈(Vector Subtraction)
- 뺄셈은 덧셈으로 표현하여 a - b = a + (-b)로 쓸 수 있습니다. 벡터연산에서도 이와 비슷한 성질이 성립합니다.
- 벡터 v의 음(negative) 벡터인 -v는 v와 길이는 같지만 방향이 반대인 벡터입니다.
- 따라서 w-v는 다음과 같이 표현할 수 있습니다.
- 또는 평행 이동 시켜서 다음과 같이 표현할 수 있습니다.
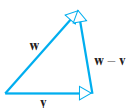
- v의 종점이 시점이 되고 w의 종점이 종점이 됩니다.
- 왼쪽이 종점, 오른쪽이 시점
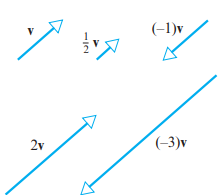
스칼라 곱셈
- -가 곱해지면 방향이 반대가 되고, 숫자는 길이를 그만큼 늘려주게 됩니다.
평행한 벡터와 동일 직선상의 벡터의 차이
- 다음은 동일 직선 위에 있는 벡터들입니다.(colinear)
- 다음은 평행한 벡터들입니다. (parallel)
- 하지만 벡터는 방향과 길이만 일치하면 모두 같은 벡터라고 했습니다. 따라서 벡터에서는 평행과 동일직선상이라는 용어가 같은 것을 의미합니다.
- 영벡터의 방향은 명확히 정의되진 않았지만 모든 벡터에 평행한 것으로 간주합니다.
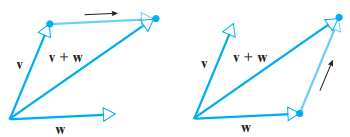
셋 이상 벡터들의 합
- 벡터 덧셈은 덧셈에 대한 결합법칙을 만족합니다.
- 벡터 u + v + w를 만드는 간단한 방법은 종점에 시점을 잇대어 연속적으로 벡터들을 나열하고 u의 시점으로부터 w의 정점을 잇는 벡터를 그리면 됩니다.
- 공통시점을 갖는 관점에서 바라보고 그려주게 된다면 세 벡터가 인접하는 세 변을 이루는 평행육면체의 대각선이라는 것을 보여줍니다.
좌표계에서의 벡터(Vectors in Coordinate Systems)(2차원, 3차원)
- 지금까지는 좌표계와 무관하게 벡터를 이야기했습니다. 이 벡터를 이제 좌표계에서 계산하게 되면 훨씬 더 간단한 것을 볼 수 있습니다.
- 벡터의 시점을 직교 좌표계의 원점으로 하면 벡터는 자신의 종점에 의해 결정되게 됩니다. 이때 이 종점의 좌표를 좌표계와 연관된 v의 성분(component)이라 부릅니다.
- 성분이 (v1, v2)인 2차원 벡터 v는 v = (v1, v2)로, 성분이 (v1, v2, v3)인 3차원 벡터 v는 v=(v1, v2, v3)으로 나타냅니다.

- 2차원 또는 3차원 벡터가 동등하기 위한 필요충분조건은 원점을 시점으로 한다면 그들의 종점이 같아야 한다는 사실이 기하적으로 입증됩니다.
- 따라서 두 벡터가 동등하기 위한 필요충분조건은 그들의 대응하는 성분들이 같다는 것입니다.
- 예를 들어 3차원 벡터 v = (v1, v2, v3)와 w = (w1, w2, w3)가 동등하기 위한 필요충분조건은 다음과 같습니다.
- v1 = w1 , v2 = w2 , v3 = w3
- 그렇다면 시점이 원점이 아닌 벡터는 어떻게 표현될까요?
- 시점 P1이 (x1, y1)이고, 종점 P2가 (x2, y2)인 벡터라면 이 벡터의 성분은 다음과 같습니다.
- 이는 벡터
 의 차입니다.
의 차입니다.
- 3차원 벡터에서도 동일하게 표현됩니다.
- 시점 P1이 (x1, y1)이고, 종점 P2가 (x2, y2)인 벡터라면 이 벡터의 성분은 다음과 같습니다.
n-공간
- n이 양의 정수일 때, n 중 순서쌍(ordered n-tuple)은 n개의 실수로 이루어진 (v1,v2,v3,..., vn)입니다. 모든 n중 순서쌍들의 집합을 n-공간이라 하고
 으로 나타냅니다.
으로 나타냅니다.  에서의 벡터연산
에서의 벡터연산
 에서의 벡터연산들은 2차원 3차원상의 벡터 연산을 자연스럽게 확장한 것입니다.
에서의 벡터연산들은 2차원 3차원상의 벡터 연산을 자연스럽게 확장한 것입니다.- 벡터의 동등
- 2차원, 3차원때와 마찬가지로 다음과 같이 정의됩니다.
- v = (v1, v2,..., vn) , w = (w1, w2,..., wn)에 대해 v1=w1, v2=w2, ... , vn=wn이면 v와 w는 동등하다(또는 같다)고 하고 v=w로 표시합니다.
- 다른 대수적 연산도 동일하게 적용됩니다.
- 일차결합
- 백터의 덧셈, 뺄셈, 스칼라 곱셈은 주로 새로운 벡터를 만들 때 혼합해서 사용됩니다.
- 예시
- 예시
- 이는 새로운 벡터 w를 v1, v2,.., vr의 일차결합(linear combination)이라 합니다.
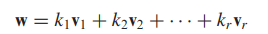
- 이때 스칼라들을 일차결합의 계수(coeeficient)라고 합니다.
- 위 정의는 앞서 배웠던 일차결합 정의와 같습니다.
- 백터의 덧셈, 뺄셈, 스칼라 곱셈은 주로 새로운 벡터를 만들 때 혼합해서 사용됩니다.
벡터의 또 다른 기호
- 지금까지 벡터를 v = (v1, v2, ..., vn)의 기호로 쓰고 쉼표로 분리된(comma-delimited) 형태로 작성하였습니다.
- 다른 표현 방식으로는 행벡터(row-vector) 또는 열벡터(column-vector) 형태가 있습니다.
- 행벡터(row-vector)
- 열벡터(column-vector)
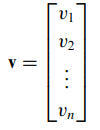
- 주로 column-vector형태로 표현하는 경우가 많습니다.
- 행벡터(row-vector)
'Math > 선형대수' 카테고리의 다른 글
| 고유값(eigenvalue)과 고유벡터(eigenvector) (3) | 2023.12.02 |
|---|---|
| 12. n차원에서의 놈(Norm), 거리(Distance), 점곱(Dot Product) (1) | 2023.11.30 |
| 10. 행렬식의 성질 / 크라머의 규칙 (1) | 2023.11.28 |
| 9. 행축소에 의한 행렬식 계산 (1) | 2023.11.28 |
| 8. 여인수 전개에 의한 행렬식(determinant) (0) | 2023.11.28 |