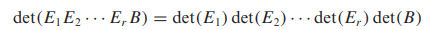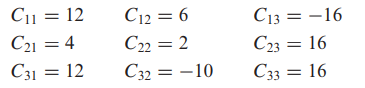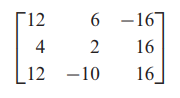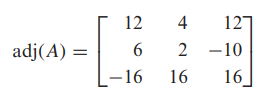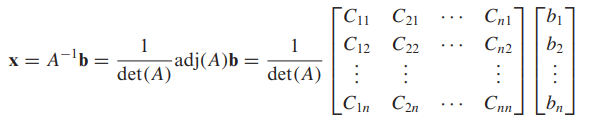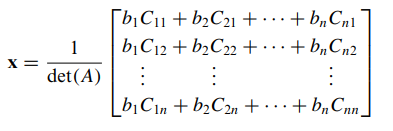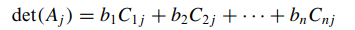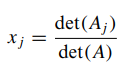목차
Elementary Linear Algebra [Anton]을 참고하여 작성하였습니다.
행렬식의 기본 성질

- 3x3 행렬 예시를 살펴보도록 하겠습니다.

- det(A+B) ≠ det(A) + det(B)
- 예시를 통해 손쉽게 확인할 수 있습니다.

- det(A) = 1
- det(B) = 8
- det(A+B) = 23
- det(A+B) ≠ det(A) + det(B)
- det(AB) = det(A)det(B)
- A가 기본행렬인 특수한 경우로 증명을 시작하겠습니다.
- 기본행렬 E를 만드는 데 사용되는 행연산과 연관한 세 가지 경우가 존재합니다.
- E가 I의 한 행에 영이 아닌 스칼라 k를 곱해서 얻은 기본행렬이라면, det(E) = k
- E가 I의 두 행을 교환하여 얻은 기본행렬이라면, det(E) = -1
- E가 I의 한 행의 상수배를 다른 행에 더하여 얻은 기본 행렬이라면 det(E) = 1
- 경우 1 [E가 I의 한 행에 영이 아닌 스칼라 k를 곱해서 얻은 기본행렬이라면, det(E) = k]
- EB는 B의 대응하는 행에 k를 곱하여 얻어진 행렬입니다.
- 따라서 det(EB) = kdet(B)가 됩니다.
- 이유 : B가 A의 한 행 또는 열에 스칼라 k를 곱해서 얻은 행렬이라면, det(B) = kdet(A)입니다.
- 이때 det(E) = k 이기 때문에 det(EB) = det(E)det(B)가 됩니다.
- 경우 2 [E가 I의 두 행을 교환하여 얻은 기본행렬이라면, det(E) = -1]
- EB는 결국 B의 행을 교환한 경우가 됩니다.
- 따라서 det(EB) = -det(B)가 됩니다.
- 이유 : B가 A의 두 행 또는 열을 교환해서 얻은 행렬이라면, det(B) = -det(A)입니다.
- 이때 det(E) = -1 이기 때문에 det(EB) = det(E)det(B)가 됩니다.
- 경우 3 [E가 I의 한 행의 상수배를 다른 행에 더하여 얻은 기본 행렬이라면 det(E) = 1]
- EB는 B의 한 행의 상수배를 해서 더해진 경우가 됩니다.
- 따라서 det(EB) = det(B)
- 이유 : B가 A의 한 행(또는 열)의 상수 배를 다른 행(또는 열)에 더해서 얻은 행렬이라면 det(B)=det(A)입니다.
- 이때 det(E) = 1 이기 때문에 마찬가지로 det(EB) = det(E)det(B)로 표현이 가능합니다.\
- 따라서 반복적으로 적용할 경우 아래처럼 적용되어서 det(AB) = det(A)det(B)가 됩니다.
- det(AB) = det(A)det(B)를 통해 새롭게 얻을 수 있는 식은 다음과 같습니다.

- 이는 B가 A의 역행렬이라고 할 경우, AB가 I가 되어 det(I)=1이 됩니다. 따라서 det(B) = 1/det(A)가 되게 됩니다.
- 정방행렬 A가 가역이기 위한 필요충분조건은 det(A) ≠ 0 입니다.
- R을 A의 기약 행사다리꼴이라고 하면 다음과 같이 표현할 수 있습니다.
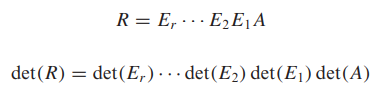
- 기본행렬의 행렬식은 0이 아니기 때문에 det(R)과 det(A)가 둘 다 0이거나 둘다 0이 아닐 것입니다.
- 만일 A가 가역일 경우 R = I가 될 것입니다. 그러므로 det(R) = 1이 될 것이고, det(A)는 0이 아니 여야 합니다.
여인수 행렬과 딸림행렬
- A가 n x n 행렬이고 Cij가 aij의 여인수이면, 다음 행렬을 A의 여인수 행렬(matrix of cofactors from A)이라고 합니다. 또한 이 행렬의 전치행렬을 A의 딸림행렬(adjoint of A)라고 합니다.
- A의 여인수 행렬(matrix of cofactors from A)
- 위 행렬의 전치행렬을 A의 딸림행렬(adjoint of A)라고 합니다.
- A의 여인수 행렬(matrix of cofactors from A)
- [예제] 딸림행렬 구하기

- A의 여인수들은 다음과 같습니다.
- 따라서 여인수 행렬은 다음과 같습니다.
- 딸림행렬은 여인수 행렬의 전치이기 때문에 다음과 같습니다.
- A의 여인수들은 다음과 같습니다.
딸림행렬을 이용한 역행렬(Inverse) 구하기

- 증명
- Aadj(A)를 살펴보면 다음과 같습니다.
- 이때 i=j가 같을 때는 여인수전개에 의해 얻은 det(A)와 같고 i ≠ j 이면 A의 제 i행 원소와 다른 행의 대응하는 원소의 여인수를 곱하여 얻은 곱들의 합이므로 0이 됩니다. 따라서 이를 정리해서 작성하게 되면 다음과 같습니다.
- 이제 A가 가역이면 det(A) ≠ 0 이기 때문에, 다음과 같이 표현할 수 있습니다.
- 양변에 A^(-1)을 곱하면 딸림행렬을 이용한 역행렬 식이 나오게 됩니다.
- Aadj(A)를 살펴보면 다음과 같습니다.
크라머의 규칙(Cramers`s Rule)
- Ax = b가 n개의 미지수와 n개의 일차방정식으로 이루어진 연립일차방정식이고 det(A) ≠ 0 이면, 연립방정식은 유일한 해를 갖는다. 이때 해는 다음과 같습니다.

- 여기서 Aj는 A의 j번째 열의 원소를 행렬 b의 원소로 대체해서 얻은 행렬입니다.
- 증명
- n>3 일 때 n개의 방정식과 n개의 미지수로 이루어진 선형계를 풀기 위해서는 크라머의 규칙보다는 가우스-요르단 소거법을 이용하는 것이 효율적입니다. 크라머의 규칙은 주로 실제적으로 해를 구하지 않고 해의 성질을 알아보는데 이용합니다.
'Math > 선형대수' 카테고리의 다른 글
| 12. n차원에서의 놈(Norm), 거리(Distance), 점곱(Dot Product) (1) | 2023.11.30 |
|---|---|
| 11. 2차원, 3차원, n차원 공간에서의 벡터 (1) | 2023.11.28 |
| 9. 행축소에 의한 행렬식 계산 (1) | 2023.11.28 |
| 8. 여인수 전개에 의한 행렬식(determinant) (0) | 2023.11.28 |
| 7. 대각 행렬, 삼각 행렬, 대칭 행렬 (1) | 2023.11.27 |