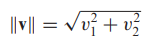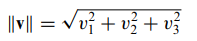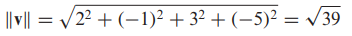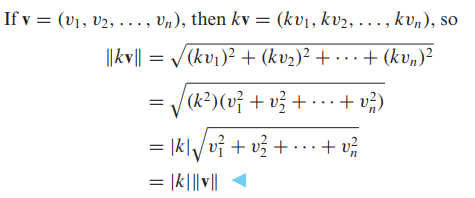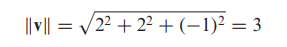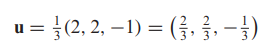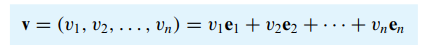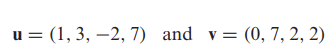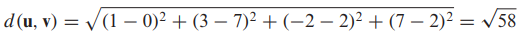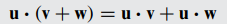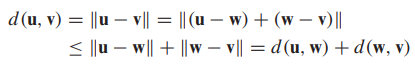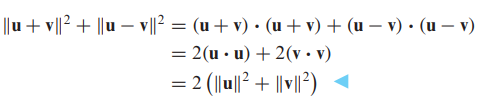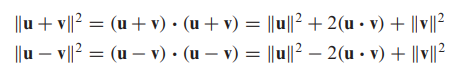목차
Elementary Linear Algebra [Anton]을 참고하여 작성하였습니다.
벡터의 놈(Norm)
- 벡터 v의 길이는 기호 ||v|| 로 나타내고 v의 놈(norm), v의 길이, 또는 v의 크기(magnitude)라고 읽습니다.
- 2차원과 3차원에서의 벡터의 놈은 피타고라스 정리에 의해 다음과 같습니다.
- 2차원
- 3차원
- 2차원
- 따라서 n차원에서의 벡터의 놈은 다음과 같이 정의됩니다.
- [예제] 놈 계산
- 놈(Norm) 정리

- (c) 증명
단위벡터(Unit Vector) / 정규화(Normalizing)
- 단위벡터(Unit Vector)
- 놈이 1인 벡터를 단위벡터(Unit Vector)라고 합니다.
- 정규화(normalizing)
- 단위벡터를 얻기 위해 영이 아닌 벡터에 자신의 길이의 역수를 곱하는 과정을 v의 정규화(normalizing v)라고 부릅니다.
- [예제] 벡터의 정규화
 와 같은 방향을 갖는 단위벡터 u를 구하기
와 같은 방향을 갖는 단위벡터 u를 구하기
표준단위벡터(Standard Unit Vector)
- 표준단위벡터(Standard Unit Vector)
- 직교좌표계 R^2(2차원), R^3(3차원)의 양의 좌표축상의 단위벡터를 표준단위벡터라고 합니다.
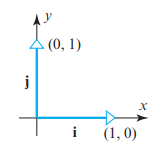
- R^2의 표준단위벡터
- i = (1,0) and j = (0,1)
- R^3의 표준단위벡터
- i = (1,0,0) and j = (0,1,0) and k = (0,0,1)

- R^n의 표준단위벡터
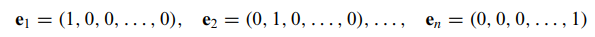
- R^n의 모든 벡터 v = (v1, v2,..., vn)은 다음과 같이 쓸 수 있습니다.
n차원에서의 거리(distance)
- 2차원
- P1(x1,y1) , P2(x2,y2)

- 3차원
- P1(x1,y1,z1), P2(x2,y2,z2)
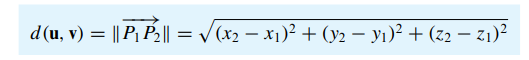
- n차원
- u = (u1, u2,..., un) , v = (v1, v2,..., vn)
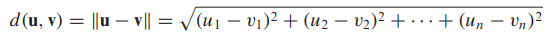
- [예제] R^n에서의 거리 계산
점곱(Dot Product)(내적)
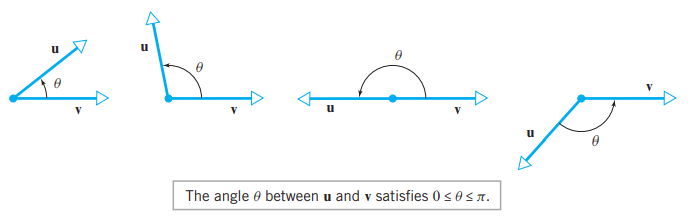
- 벡터 u, v 사이의 각(angle)은 크기가 0<= θ <= π 인 u, v에 의해 결정되는 각 θ 입니다.
- u와 v의 점곱(dot product), 또는 유클리드 내적(Euclidean inner product)은 u · v로 나타내고 다음과 같이 정의됩니다.

- cos θ에 관해서 표현하면 다음과 같이 표현이 가능합니다.

- 따라서 다음과 같이 내적의 부호에 따라 θ가 예각인지 둔각인지 직각인지 알 수 있습니다.

- acute angle : 예각 / obtuse angle : 둔각 / right angle : 직각
- cos θ에 관해서 표현하면 다음과 같이 표현이 가능합니다.
- 증명
- 제2 코사인법칙을 통해 증명이 가능합니다.

- [예제] 내적 구하기

- u · v = 0x0 + 0x2 + 1x2 = 2
- 또는 크기와 각도를 이용해서 풀 수 있습니다.
- ||u|| = 1 , ||v|| = 2 √ 2
- cos(45◦ ) = 1/ √ 2
- 결론 : u · v = u v cos θ = (1)(2 √ 2)(1/ √ 2) = 2
점곱(내적)의 대수적 성질
- 대칭성
- 분배성
- [예제] 점곱 계산
R^n에서의 코시-슈바르츠 부등식(Cauchy–Schwarz Inequality)과 각
- cos θ 의 범위는 -1부터 1 사이이므로 다음과 같이 표현할 수 있습니다.
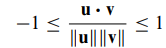
- 이를 통해 코시-슈바르츠 부등식이 생겨나게 됩니다.
- 코시-슈바르츠 부등식(Cauchy-Schwarz Inequality)
R^n(n차원)의 기하학
- 평면기하에서의 성질을 통해 다음 정리들이 유도됩니다.
 (삼각형, Triangle)
(삼각형, Triangle)

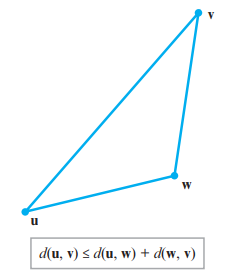
- 증명
 (평행사변형, Parallelogram)
(평행사변형, Parallelogram)

- 증명
- 유클리드 내적을 다르게 표현하면 다음과 같이 표현할 수 있습니다.

- 증명
- 증명
'Math > 선형대수' 카테고리의 다른 글
| 고유값(eigenvalue)과 고유벡터(eigenvector) (3) | 2023.12.02 |
|---|---|
| 11. 2차원, 3차원, n차원 공간에서의 벡터 (1) | 2023.11.28 |
| 10. 행렬식의 성질 / 크라머의 규칙 (1) | 2023.11.28 |
| 9. 행축소에 의한 행렬식 계산 (1) | 2023.11.28 |
| 8. 여인수 전개에 의한 행렬식(determinant) (0) | 2023.11.28 |