이항 분포(Binomial Distribution)

 

목차

• 이항분포(binomial distribution)

이항분포(binomial distribution)

• 이항분포는 이산 확률분포 중 하나입니다.
• 이항분포는 성공 확률이 p이고 실패 확률이 1−p인 독립적인 시도를 n번 반복했을 때, 성공하는 횟수의 분포를 나타냅니다. (꼭 성공/실패가 아니더라도 앞/뒤 등 두 가지를 가지면 됩니다.)
  • 베르누이 시행을 n번 반복하는 것입니다.
  • 베르누이 시행(Bernoulli trial 또는 binomial trial)은 확률론과 통계학에서 임의의 결과가 '성공' 또는 '실패'의 두 가지 중 하나인 실험을 뜻합니다.
• 이항분포의 확률 질량함수
  • 
  • n(시도 횟수) : 독립적인 시도를 몇 번 반복하는지 나타냅니다.
  • p(성공 확률) : 각 시도에서 성공할 확률입니다.
  • X(성공 횟수) : n번의 시도 중 성공하는 횟수를 나타내는 확률 변수입니다.
• 왜 nCk 조합이 사용될까?
  • n번의 시도 중에서 k개가 선택되는 것이라고 생각하면 됩니다. 근데 그 k개가 선택되는 것들이 모두 똑같이 성공을 의미하는 것이기 때문에 순열이 아닌 조합으로 nCk가 사용됩니다.
  • 예를 들어 5개 중에 2개를 선택하는 경우가 있다고 한다면 XXXXX 가 있을 때 이 중에서 2개를 선택하는 것입니다. OOXXX, OXOXX, ..., XXXOO 모두 가능하며, 이때는 OO를 택할 때 순서를 고려하지 않기 때문에 순열이 아닌 조합의 경우의 수만큼 존재하게 됩니다.
• 이항분포는 종종 B(n,p) 또는 Bn(n,p)와 같은 형식으로 표현됩니다.
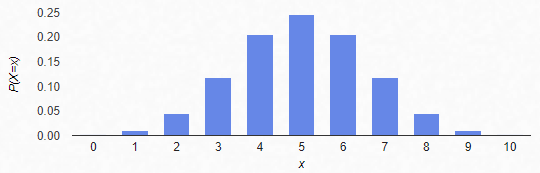
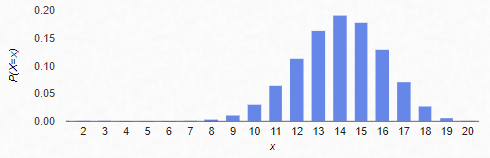
• 이항분포의 다양한 예시
  • (n=10, p=0.5)
    • 
  • (n=20, p=0.5)
    • 
  • (n=10, p=0.7)
    • 
  • (n=20, p=0.7)
    •