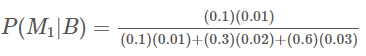베이즈 정리(Bayes' theorem)

 

목차

 

 

베이즈 정리 

• 베이즈 정리는 단순히 조건부 확률을 뒤집어서 생각하는 역문제 해결(ex. 의료진단)에서 사용할 수 있지만, 주로 사전확률갱신(ex. 그 사람이 날 좋아할까?)에서 자주 사용됩니다.
• 데이터를 기반으로 한 분석이 가능해진 현대에 와서 그 강력함이 재조명되었습니다. 베이즈 정리를 통해 데이터가 많을수록 올바른 의사결정을 내릴 확률이 높아지기 때문입니다.(자세한 이유는 "그 사람이 날 좋아할까?" 예시를 보면 알 수 있습니다.)
• 수식 (이 수식은 조건부 확률을 전개해 보면 어떻게 나온 지 유도가 가능합니다.)
  
  • 
  • P(A∣B) : (사후 확률(Posterior probability) : 증거 B가 주어졌을 때 사건 A의 확률)
  • P(B∣A) : (우도(Likelihood) : 사건 A가 주어졌을 때 증거 B가 관측될 확률)
  • P(A) : (사전 확률(Prior probability) : 추가 정보나 증거 없이 사건 A의 확률) 
  • P(B) : (증거의 확률(Evidence) : 모든 가능한 사건 A에 대해 고려하여 증거 B가 관측될 확률)
    • 설명만 보면 P(B|A)와 P(B)가 같은 말처럼 들리는데 P(B)는 이제 모든 가능한 A의 사건에 대한 P(A) x P(B|A)의 합입니다. (즉, 베이즈 정리의 적용 과정에서 P(B)는 모든 가능한 사건 A에 대한 P(B|A)와 P(A)의 곱의 합으로 나타낼 수 있습니다.)
    • 
• 예시 (예시를 보다보면 베이즈 정리가 왜 사용되는지 이해가 되기 때문에 예시를 위주로 작성하였습니다.)
  • 불량률 검사
    • 한 공장에서 어떤 제품을 생산할 때 M1, M2, M3 기계를 사용합니다. 각 기계는 전체 생산량의 10%, 30%, 60%를 차지하고 있습니다. 모든 기계는 불량이 발생할 수 있는데, 각 기계의 불량률은 1%, 2%, 3%입니다.(각 기계를 사용했을 때, 불량률) 불량품이 발생했을 때, 기계 M1에서 발생했을 확률을 구하시오. (즉, P(M1|불량품발생)을 구하시오.)
    • 분모에 해당하는 P(불량품발생) 확률은 P(불량품발생|M1) x P(M1) + P(불량품발생|M2) x P(M2) + P(불량품발생|M3) x P(M3)를 통해서 구할 수 있습니다. (즉, 모든 생산 기계의 불량품발생확률들을 구하고 합해주기) 
    • 분자에 해당하는 P(M1, 불량품발생)을 바로 구할 수가 없습니다. P(불량품발생|M1)과 P(M1)이 주어져있기 때문에 이를 이용하여 P(불량품발생|M1) x P(M1)을 통해 P(M1, 불량품발생)을 구할 수 있습니다.
    • 수식
      • 
      • 
  • 의료진단 (사건 = 병존재 / 증거 = 양성(테스트 결과)) [역문제 해결의 대표적인 예시]
    • 현재 병의 발병률과, 병이 있을때 검사가 양성을 보이는 확률(병이 아닐 때 검사가 양성일 확률도 가지고 있습니다. 즉 양성을 보이는 모든 경우의 각 확률 값을 가지고 있습니다.)을 가지고 있습니다. 이제 이를 토대로 양성일 때 병이 있을 확률을 계산하고 싶습니다. 이럴 경우 사용하는 방법이 베이즈 정리입니다.
      • 병의 발병률 = 0.01(1%) (=P(병))  (즉, 병이 없을 확률은 0.99(99%))
      • 병이 있을 때 검사가 양성을 보이는 확률 = 0.97(97%) (=P(양성|병))
      • 병이 없을 때 검사가 양성을 보이는 확률 = 0.02(2%) (=P(양성|병x))
    • 양성일 때 병이 있을 확률 (=P(병|양성)) 계산하기
      • P(병|양성)
        • = ( P(양성|병) x P(병) ) / P(양성)
        • = ( P(양성|병) x P(병) ) / ( P(양성|병) x P(병) + P(양성|병x) x P(병x) )
      • 
  • "그 사람이 날 좋아할까?" [사전확률갱신의 대표적인 예시]
    • 그 사람이 날 좋아한다고 판단할만한 증거들이 주어지면, 그 증거들을 기반으로 그 사람이 날 좋아하는지에 대한 확률을 업데이트해 나아가는 과정입니다. (예를 들면, 초콜릿을 받은 일, 단 둘이 식사를 한 일, 밤늦게까지 통화를 한 일 등을 통해 사전확률을 지속적으로 업데이트합니다.)
      • 증거가 많을수록 사전확률 업데이트는 더 많이 되고 그 사람이 날 좋아하는지 더 확실하게 알 수 있게 됩니다.
      • 처음 사전 확률은 아무런 정보가 없기 때문에 확률을 동등하게 생각해서 50%로 가정합니다. 때문에 증거가 많아야 처음 가정한 확률 50%에서 더 정확한 확률로 변화하게 될 것입니다.
    • 먼저 그 사람이 나에게 초콜릿을 준 사건이 발생했습니다. 이를 토대로 초콜릿을 준 사람은 나를 얼마큼 좋아할까(=P(좋아함|초콜릿을줌))를 계산해보고 싶습니다.
      • 
      • 이를 계산하기 위해서는 사람을 좋아할 때 초콜릿을 줄 확률과 좋아하지 않지만 초콜릿을 줄 확률을 알아야 합니다. (또는 사람을 좋아할 때 초콜릿을 줄 확률과 그냥 단순히 초콜릿을 줄 확률을 알아야 합니다.)
        • 
        • 그 사람을 좋아할 때 초콜릿을 줄 확률은 0.4이고, 그 사람을 좋아하지 않을 때 초콜릿을 줄 확률은 0.3입니다. 이를 전체 1이라는 확률에서 표현해 보면 아래와 같습니다.
        • 
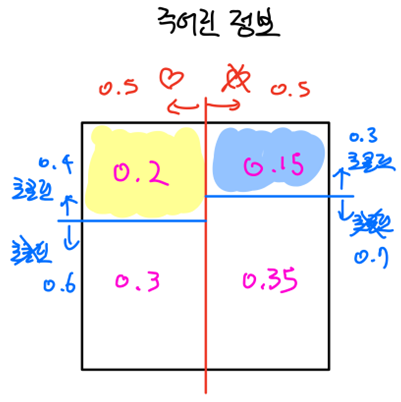
      • 이제 여기서 주목해야 할 것은 초콜릿을 줬을 때 좋아할 확률이기 때문에 노란색 영역과 파란색 영역을 살펴봐야 합니다. 그 영역에 대한 조건부확률 P(좋아함|초콜릿)을 구하면 다음과 같습니다.
        • 
        • 즉, 이 과정을 살펴보면 왜 베이지 공식과 같은 수식이 나오게 되었는지 알 수 있습니다.
    • 이제 여기서 멈추지 않고, 그 사람과 단둘이 밥까지 먹게 되었습니다. 이제 그 사람이 나를 얼마나 좋아하는지를(=P(좋아함|밥)) 계산해 보겠습니다.
      • 먼저 각 필요한 각 확률들을 조사해 보았습니다.
        • 어떤 사람을 좋아할 때 단둘이 밥을 먹을 확률을 조사해 본 결과 0.7이었고, 좋아하지 않는데 그 사람과 단둘이 밥을 먹을 확률은 0.35이었습니다.
        • 현재 초콜릿을 받은 상태에서 그 사람이 나를 좋아할 확률(=사전확률)은 0.57입니다.
        • 이를 전체 1이라는 확률에서 표현해 보면 아래와 같습니다.
        • 
      • 마찬가지로 단둘이 밥을 먹었을 때 좋아할 확률이기 때문에 노란색 영역과 파란색 영역을 살펴봐야 합니다. P(좋아함|밥)을 구해보면 다음과 같습니다.
        
        • 
    • 이처럼 정보가 많을수록 사전확률이 계속 업데이트되어 그 사람이 나를 좋아하는지 좀 더 정확하게 판단할 수 있게 됩니다.

요약 : 베이즈 정리는 역문제를 해결하거나 사전확률갱신과 같은 상황에서 사용합니다.

참고

• https://hsm-edu.tistory.com/ 
• https://m.post.naver.com/viewer/postView.naver?volumeNo=28293397&memberNo=41516152