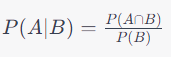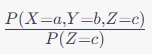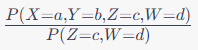목차
결합 확률과 주변 확률
- 확률변수 X, Y에 대해, X=a고 Y=b가 될 확률은 P(X=a, Y=b) (또는 P(X=a∩ Y=b) )입니다. 이런 식으로 여러 조건을 지정하고 모든 조건이 동시에 성립하는 확률을 결합 확률이라고 부릅니다.
- 결합 확률과 대비해서 P(X=a)나 P(X=b) 같은 단독 확률은 주변 확률이라고 부릅니다.
- 주변 확률이라는 용어는 상대적입니다. X, Y, Z의 결합분포에서 보면 P(Y=b, Z=a)도 주변확률이 됩니다. 그와 동시에 P(Y=b, Z=a) 자체는 Y=b와 Z=a의 결합 확률이기도 합니다.
- 결합 확률과 주변 확률의 관계
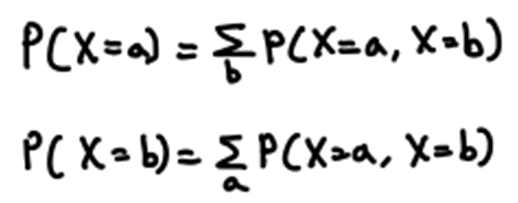
- 결합 확률들의 집합이 결합분포, 주변 확률들의 집합이 주변분포입니다.
- 참고 : 결합분포에서 주변분포를 계산할 수 있지만 주변분포가 지정됐다고 해서 그것으로 결합분포를 결정할 수 없습니다.
- 아래 예시를 보면 주변분포가 같지만, 결합분포는 다르다는 것을 확인할 수 있습니다. 이를 통해 주변분포가 지정됐다고 그것으로 결합분포를 결정할 수 없다는 것을 간접적으로 알 수 있습니다.
- P(X=빨강) = P(X=빨강, Y=숫자) + P(X=빨강, Y=그림)을 통해서 결합분포를 통해 주변분포를 계산할 수 있습니다.
- 참고 : 결합분포에서 주변분포를 계산할 수 있지만 주변분포가 지정됐다고 해서 그것으로 결합분포를 결정할 수 없습니다.
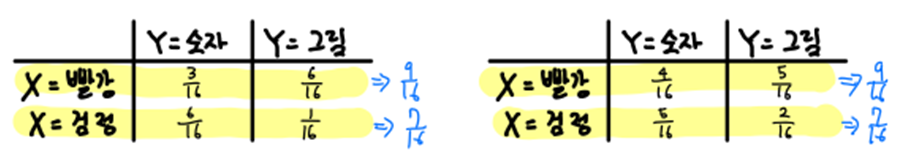
요약 : 결합확률은 두 개 이상의 확률변수가 동시에 특정 값을 가질 확률을 나타냅니다. 주변확률은 결합확률 안의 확률변수를 의미하는 것이며, 상대적인 용어입니다. P(X=a, Y=b)라고 한다면 이것은 결합확률이면서 누군가의 주변확률이 될 수도 있습니다.
조건부 확률
- 조건부 확률은 어떤 사건 B가 주어졌을 때, 다른 사건 A가 발생할 확률을 나타냅니다. 이를 수식으로 나타내면, P(A|B)가 됩니다. 이는 P(A, B)/P(B)로 계산됩니다. (P(A, B)는 사건 A와 B가 동시에 발생하는 결합확률을 나타냅니다.)
- 다시 말하면 조건이 주어지면 그 조건을 전체 면적 1로 본다는 것입니다. 아래 예시를 통해 조건부 확률을 계산해 보도록 하겠습니다.
- P(Y=숫자 | X=빨강)
- P(X=빨강) = 9/16
- P(Y=숫자, X=빨강) = 3/16
- 따라서 P(Y=숫자 | X=빨강) = 3/9 = 1/3 이 됩니다.
- 이론적으로 계산하면 위와 같이 계산해야 하지만, 조건을 확률 전체 1로 생각하면 다소 쉽게 생각할 수 있습니다. X=빨강이라는 것을 전체 면적 1로 생각하면, 그중에서 숫자가 차지하는 면적을 계산하는 것과 동일합니다. 이런 식으로 생각하면 위와 같은 연산과정이 왜 발생했는지 쉽게 이해할 수 있습니다.
- P(Y=그림 | X=빨강)
- 이 예시도 마찬가지로 전체 빨강 중에 그림이 차지하는 면적을 계산하면 됩니다.
- 즉 6/9 = 2/3가 될 것입니다.
- P(Y=숫자 | X=빨강)

- 세 개 이상의 확률변수의 조건부 확률
- 다음과 같이 쉼표가 여러 개가 있고 조건부 확률 기호까지 있을 때는 조건부 확률 기준으로 무조건 오른쪽은 모두 조건이라고 생각하면 됩니다.
- P(X=a, Y=b | Z=c)
- P(X=a | Y=b, Z=c)
- P(X=a, Y=b | Z=c, W=d)
- 조건부 확률은 결합확률과 헷갈릴 수 있기 때문에 문장해석을 잘해야 합니다. 보통 일반적으로 "중", "조건", "~때"와 같은 표현은 조건부 확률을 나타내는 문장 구조에서 자주 사용됩니다.
- 예를 들어 어떤 공장의 A, B, C 기계가 있다고 할 때, 각 기계의 불량품 생산율이 1%,2%,5%라고 합니다. 이럴 경우 이거는 P(불량품|A) 인지 P(불량품, A)인지 헷갈릴 수가 있습니다. 헷갈리지 않기 위해서는 문장해석을 잘해야 합니다.
- "A기계가 생산한 제품 중 불량품의 비율", "A기계를 사용할 때 불량품이 나올 확률", "A기계가 제품을 생산했을 때 불량품이 나올 확률"과 같은 표현은 조건부 확률 P(불량품|A)를 의미합니다.
- "A제품을 사용했으면서 불량품인 확률"과 같은 표현은 결합확률 P(불량품, A)를 의미합니다.
- 위의 예시에서는 각 기계의 불량품 생산율이라고 했기 때문에 각 기계를 전체 면적으로 보게 되는 조건부 확률이 되는 것입니다.
- 또 다른 예시로 전체 학생 중에서 수학을 좋아하는 여학생의 비율과, 여학생 중에서 수학을 좋아하는 학생의 비율이 있습니다.
- 전체 학생 중에서 수학을 좋아하는 여학생의 비율이라고 한다면 조건이 전체 학생이 되는 것입니다. 하지만 문제에서 모든 조건들을 전체 학생 중에서 수학을 좋아하는 비율 / 전체 학생 중 여학생 비율 이런 식으로 전체 학생별로 작성되어 있다면 전체 학생이라는 조건을 생략하고 단순히 결합확률로 작성해도 됩니다. ( P(수학 좋아함, 여학생) )
- 여학생 중에서 수학을 좋아하는 학생의 비율이라고 한다면 조건이 여학생이 되는 것입니다. 따라서 여학생이 조건인(즉 여학생이 전체 면적으로 설정되는) 조건부 확률이 됩니다.
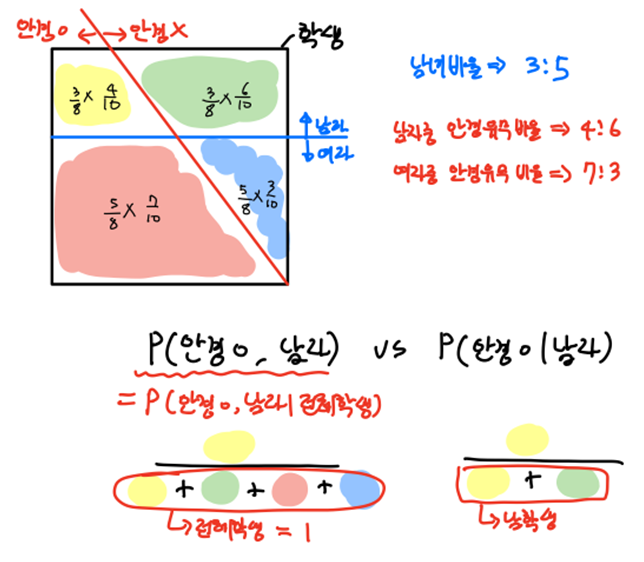
- 마지막으로 그림을 통해서 조건부 확률과 결합확률의 확실한 차이를 살펴보도록 하겠습니다.
- 예를 들어 어떤 공장의 A, B, C 기계가 있다고 할 때, 각 기계의 불량품 생산율이 1%,2%,5%라고 합니다. 이럴 경우 이거는 P(불량품|A) 인지 P(불량품, A)인지 헷갈릴 수가 있습니다. 헷갈리지 않기 위해서는 문장해석을 잘해야 합니다.
조건부 확률을 이용한 결합확률의 분해
- 참고 : 아래 표현에서 P(X), P(Y) 같은 경우, 확률변수 가 어떠한 특정한 상태(예를 들면 x, y)를 취할 확률을 의미합니다
- 조건부 확률은 결합확률을 해당 조건의 확률로 나누어서 계산하였습니다. 이번에는 반대로 결합확률을 조건부 확률을 이용하여 표현해 보도록 하겠습니다.
P(X, Y)=P(X∣Y) × P(Y)
- 이번에는 세 개 이상의 결합확률을 분해해 보도록 하겠습니다.
- P(X, Y, Z)=P(X∣Y, Z) × P(Y∣Z) × P(Z)
- 그 과정을 살펴보면 먼저 P(X, Y, Z)를 다음과 같이 분해할 수 있습니다. P(X, Y, Z)=P(X∣Y, Z) × P(Y, Z) 이제 다시 P(Y, Z)를 분해하면 다음과 같이 나오게 됩니다. P(Y, Z)=P(Y∣Z) × P(Z) 따라서 결론적으로 위의 식과 같이 나오게 됩니다.
- 상황에 따라서는 이런 조건부 결합분포의 분해도 활용될 수 있습니다.
- P(X , Y | Z) = P(X | Y , Z) × P(Y | Z)
- P(U, V, W, X | Y, Z) = P(U, V | W, X, Y, Z) × P(W | X, Y, Z) × P(X | Y, Z)
- 전체를 분자, 오른쪽에 있는 것을 분모라고 생각하면 쉽게 연산이 가능합니다.
- 즉 (U, V, W, X, Y, Z) / (Y, Z) = ( (U, V, W, X, Y, Z) / (W, X, Y, Z) ) × ( (W, X, Y, Z) / (X, Y, Z) ) × ( (X, Y, Z) / (Y, Z) )
- 여기서 이제 의문점이 듭니다. 그럼 결합확률을 왜 조건부 확률로 분해할까? 실제로 많은 상황에서 결합확률을 바로 계산하는 것이 간단하고 효과적일 수 있습니다. 그러나 다음과 같은 이유로 결합확률을 조건부 확률로 분해하는 것이 유용할 때도 있습니다.
- 정보의 제한 : 때로는 특정 조건부 확률에 대한 정보만 주어져 있어서 결합확률을 바로 계산할 수 없을 때가 있습니다. 이럴 때 조건부 확률을 활용하여 결합확률을 유도하는 것이 필요합니다.
- 독립성 : 두 확률변수가 독립적인지 아닌지를 판단할 때, 조건부 확률과 결합확률의 관계를 검토하는 것이 도움이 됩니다. 만약 두 확률 변수가 독립적이면, 결합확률은 각 변수의 주변확률의 곱과 같아집니다.
- 계산의 단순화 : 복잡한 문제에서는 조건부 확률을 사용하여 문제를 여러 단계로 나누어 단순화시키는 것이 계산을 쉽게 만들 수 있습니다.
요약 : 조건부 확률은 특정한 조건을 전체 면적 1로 보고 그 안에서 특정상황의 확률을 계산하는 것입니다.
'Math > 확률과 통계' 카테고리의 다른 글
| 이항 분포(Binomial Distribution) (1) | 2023.10.11 |
|---|---|
| 순열과 조합(Permutation & Combination) (0) | 2023.10.11 |
| 확률에서 독립(Independent) (1) | 2023.10.10 |
| 베이즈 정리(Bayes' theorem) (0) | 2023.10.08 |
| 확률 기본(확률변수, 확률분포)(Probability Basic(Random Variable, Probability Distribution)) (0) | 2023.10.07 |