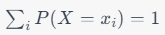목차
확률이란?
- 확률은 면적입니다. 전체 면적은 1입니다.
- 확률은 면적이기 때문에 음수가 되는 일은 없습니다.
- 확률은 전체 면적 1을 구분해 칠할 수 있는 영역의 면적입니다.
- 확률변수(Random Variable, X)는 실험 결과나 관측 결과와 같은 랜덤 한 사건의 결과를 실수로 매핑하는 함수입니다.(꼭 실수가 아니어도 됩니다. 예를 들어, 동전 던지기 실험에서 "앞면" 또는 "뒷면"처럼 확률변수의 결과가 실수가 아닐 수도 있습니다. 하지만 편의를 위해 "앞면"을 1로, "뒷면"을 0과 같이 실수로 매핑하여 표현합니다.)
- 이산 확률변수 (Discrete Random Variable):
- 한정된 개수의 명확한 값을 가집니다.
- 각 값은 특정 확률을 가집니다.
- 예시: 주사위 던지기 (결과값: 1, 2, 3, 4, 5, 6), 동전 던지기 (결괏값: 앞면, 뒷면)
- 연속 확률변수 (Continuous Random Variable):
- 연속된 범위 내의 무한한 개수의 값을 가질 수 있습니다.
- 특정 한 값을 가질 확률은 0입니다. 대신, 값의 범위 (예: 사람의 키가 170cm에서 171cm 사이일 확률)에 대한 확률을 계산할 수 있습니다.
- 예시: 사람의 키 (결과값: 특정 범위 내의 모든 실수), 온도 측정 (결괏값: 특정 범위 내의 모든 실수)
- 연속 확률변수는 범위를 나눈다든지 하는 방식( 키를 예시로 들면 0.1cm )으로 "이산화"할 수 있습니다.
- 이산 확률변수 (Discrete Random Variable):
- 확률분포(Probability Distribution)는 확률변수가 취할수 있는 각 값에 대한 확률을 설명합니다.
- 이산 확률변수(Discrete random variable)의 확률 분포
- 이산 확률변수(Discrete random variable)의 경우 확률분포는 확률질량함수(PMF, Probability Mass Function)로 표현됩니다. PMF는 확률변수가 특정 값 x를 취할 확률을 나타냅니다. P(X=x)
- 모든 가능한 값 x_i에 대한 확률 P(X=x_i)의 합은 1이 됩니다.
- 예시: 주사위 던지기
- 확률변수 X의 결과는 {1, 2, 3, 4, 5, 6}
- 확률분포를 표현하는 확률질량함수(PMF)는 다음과 같습니다:
- P(X=1) = 1/6
- P(X=2) = 1/6
- ...
- P(X=6) = 1/6
- 각 값에 대한 확률을 직접 알 수 있습니다.
- 연속 확률변수(Continuous random variable)의 확률 분포
- 연속 확률변수(Continuous random variable)의 경우 확률분포는 확률밀도함수(PDF, Probability Density Function)로 표현됩니다. 특정 값에서의 PDF의 값 자체는 확률이 아니며, 값을 구간으로 지정하고 그 구간에 대한 확률(면적)을 계산하여 확률을 나타냅니다.
- 확률밀도함수 아래의 전체 면적(즉, 함수의 전체 범위에 대한 적분 값)은 1이 됩니다.
- 예시: 어떤 도시의 하루 최고 기온 측정
- 확률변수 X의 결과는 예를 들면 20°C ~ 35°C 사이의 어떤 값을 취할 수 있습니다.
- 이 범위 내의 특정 기온, 예를 들어 27°C의 확률은 0입니다. 왜냐하면 연속 확률변수에서는 특정한 값에 대한 확률을 0으로 정의합니다.
- 그러나 확률밀도함수(PDF)를 사용하여 특정 범위의 확률을 알 수 있습니다. 예를 들어, 27°C에서 28°C 사이의 기온이 될 확률은 PDF 아래의 그 구간의 면적으로 계산됩니다.
- 이산 확률변수(Discrete random variable)의 확률 분포
요약 : 확률은 확률변수가 취할 수 있는 특정한 값(또는 범위)에 대한 확률분포에서의 비율 또는 면적으로 정의됩니다.
'Math > 확률과 통계' 카테고리의 다른 글
| 이항 분포(Binomial Distribution) (1) | 2023.10.11 |
|---|---|
| 순열과 조합(Permutation & Combination) (0) | 2023.10.11 |
| 확률에서 독립(Independent) (1) | 2023.10.10 |
| 베이즈 정리(Bayes' theorem) (0) | 2023.10.08 |
| 결합 확률, 주변 확률, 조건부 확률(Joint Probability, Marginal Probability, Conditional Probability) (1) | 2023.10.08 |