목차
정의
- 손실 함수를 최소화하는 모델의 파라미터를 찾기 위해, 최적화(Optimization) 알고리즘을 사용합니다.
- 경사 하강법(Gradient Descent)은 최적화 알고리즘 중에 대표적인 방법입니다.
- 손실 함수의 Gradient(미분값)을 사용하여 파라미터를 반복적으로 업데이트를 진행합니다.
- 경사 하강법을 진행하기 위해서는 손실 함수가 볼록(Convex)해야 전역 최솟값(Global Minima)에 손쉽게 찾아갈 수 있습니다.
- 비볼록(Non-Convex) 함수에서 경사 하강법은 지역 최솟값(Local Minima) 등에 갇힐 위험이 있습니다.
- 로지스틱 회귀에서 MSE loss를 사용하지 않고, Binary Cross Entropy(=BCE)를 사용하는 이유도 Convex 하게 만들어주기 위함입니다.
- 선형 회귀에서 MSE loss 함수는 Convex 하지만, 로지스틱 회귀에서 MSE를 사용하면 Non-Convex 해질 수 있습니다. 이는 로지스틱 회귀에서 시그모이드 함수가 포함되기 때문인데, 이로 인해 최적의 해를 찾기가 어려워질 수 있습니다. 이 때문에 로지스틱 회귀에서는 주로 Binary Cross Entropy(BCE) 손실 함수를 사용합니다. BCE 손실 함수는 Convex 하기 때문에 전역 최솟값을 찾는 것이 보장됩니다.
- 선형 회귀에서 MSE loss 함수는 Convex 하지만, 로지스틱 회귀에서 MSE를 사용하면 Non-Convex 해질 수 있습니다. 이는 로지스틱 회귀에서 시그모이드 함수가 포함되기 때문인데, 이로 인해 최적의 해를 찾기가 어려워질 수 있습니다. 이 때문에 로지스틱 회귀에서는 주로 Binary Cross Entropy(BCE) 손실 함수를 사용합니다. BCE 손실 함수는 Convex 하기 때문에 전역 최솟값을 찾는 것이 보장됩니다.
- 어떤 함수가 Convex한지 확인하는 방법은 다음과 같습니다.
- 손실 함수 f(x)가 어떤 구간에서 2차 도함수 f′′(x)가 항상 양수라면, 해당 구간에서 함수 f(x)는 볼록함수(convex function)입니다.
- 여러 변수를 가진 함수의 경우, 그 함수의 헤시안 행렬(Hessian matrix)이 positive semi-definite이라면, 그 함수는 볼록함수입니다.
경사 하강법의 과정
- 초기화 : 모델의 파라미터를 임의의 값으로 초기화합니다.
- Gradient 계산 : 현재의 파라미터 값에서 손실 함수의 그래디언트(변수별 편미분값)를 계산합니다.
- 파라미터 업데이트 : 계산된 그래디언트를 사용하여 파라미터를 업데이트합니다. 파라미터는 다음과 같이 업데이트됩니다. ( 는 학습률(learning rate)이라고 하며, 업데이트의 정도를 결정합니다.)

- 반복 : 수렴(convergence)할 때까지 그래디언트 계산과 파라미터 업데이트를 반복합니다.
간단한 그림을 통한 경사 하강법의 이해
- 손실 함수가 볼록하다고 가정하고 손실 함수를 최소화하는 모델의 파라미터를 찾아가는 과정을 간단하게 설명하겠습니다.
- 실제로는 모델의 파라미터가 무수히 많지만, 단순하게 표현하기 위하여 파라미터를 w가 하나만 있다고 가정하고 살펴보겠습니다.
- [기울기가 양수인 지점]

- [기울기가 음수인 지점]

- 즉, 손실 함수가 볼록할 경우 어느 지점에 있든지 경사하강법을 적용하면 손실함수가 최소인 지점으로 이동하게 됩니다.
- 여기서 하나 더 중요한 점을 알 수 있습니다. 그것은 learning rate 값 설정의 중요성입니다.
- 만약에 learning rate를 너무 작게 설정한다면, 기울기 값에 곱해지는 값이 너무나도 작아서 아주 조금씩 파라미터 값이 이동하게 되어 최소 지점으로 이동하기에 많은 시간이 걸릴 것입니다.

- 반대로, learning rate를 너무 크게 설정한다면, 기울기 값에 곱해지는 값이 너무나도 커져서 최소 지점으로 이동하는 것이 아닌 발산하는 현상이 발생하게 됩니다.
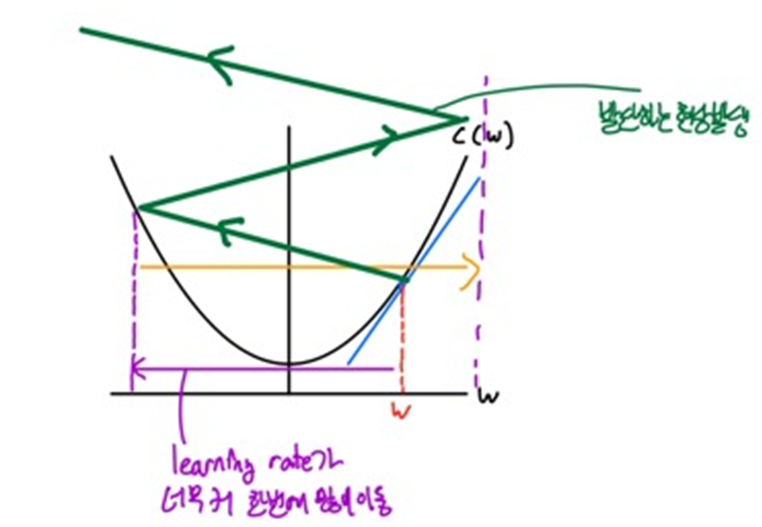
- 이를 통해 적절한 learning rate 값을 선정하는 것이 중요하다는 것을 알 수 있습니다.
- 만약에 learning rate를 너무 작게 설정한다면, 기울기 값에 곱해지는 값이 너무나도 작아서 아주 조금씩 파라미터 값이 이동하게 되어 최소 지점으로 이동하기에 많은 시간이 걸릴 것입니다.
여러 종류의 경사 하강법
- 배치 경사 하강법(Batch Gradient Descent)
- 전체 훈련 데이터셋에 대해 그래디언트를 계산합니다.
- 확률적 경사 하강법(Stochastic Gradient Descent, SGD)
- 각 반복마다 하나의 샘플에 대해 그래디언트를 계산합니다.
- 미니배치 경사 하강법(Mini-batch Gradient Descent)
- 각 반복마다 일정 개수의 샘플에 대해 그래디언트를 계산합니다.
'AI > Basic' 카테고리의 다른 글
| 대표적인 Activation Function (Sigmoid, tanh, ReLU, Leaky ReLU, ELU, PReLU, Softplus, Swish) (0) | 2023.11.21 |
|---|---|
| 신경망 기초 (0) | 2023.11.10 |
| 손실 함수(Loss Function) (0) | 2023.09.28 |
| 손실 함수(Loss function) vs 비용 함수(Cost function) (0) | 2023.09.28 |
| 로지스틱 회귀(Logistic Regression) (0) | 2023.09.28 |



