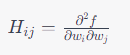목차
정의
- 손실 함수는 모델의 예측값과 실제값이 얼마나 잘 일치하는지를 측정하는 함수입니다.
- 손실 함수의 값이 작을수록 모델의 예측이 정확하다고 볼 수 있습니다.
- 손실 함수를 최소화하는 모델의 파라미터를 찾는 것이 모델의 학습 과정의 핵심입니다.
- 선형 회귀나 로지스틱 회귀의 경우는 학습 데이터에 대해 손실함수가 최소화되는 w0, w1, w2, ..., wn 값을 찾는 것이 모델의 학습 과정입니다.
- 손실 함수를 최소화하는 모델의 파라미터를 찾기 위해 대표적으로 경사 하강법(Gradient Descent)이라는 최적화 (Optimization) 알고리즘을 사용합니다. 경사 하강법의 내용은 아래 내용을 참고해 주시길 바랍니다.
- 비용 함수라고도 말하는 경우가 있는데, 두 용어의 차이점은 아래 내용을 참고해 주시길 바랍니다.
- 손실 함수를 최소화하는 모델의 파라미터를 찾기 위해서 경사하강법을 사용한다고 했습니다. 하지만 여기서 완벽히 전역 최솟값에 도달하기 위해서는 전제 조건이 필요합니다. 손실 함수가 Convex 해야 한다는 점입니다. (Convex = 아래로 볼록, Concave = 위로 볼록) 하지만 많은 딥러닝문제에서는 비볼록(non-convex) 손실 함수를 자주 사용하게 됩니다. 심층 신경망에서는 비선형 활성화 함수와 복잡한 네트워크 구조로 인해 모든 매개변수에 Convex 한 손실 함수는 거의 존재하기 힘들기 때문입니다.
- Convex 하지 않은 손실함수를 적용하게 되면 경사하강법을 적용할 때, 제대로 된 방향성을 찾지 못해 학습이 제대로 이루어지지 않게 될 수 있습니다.
- 이럴 경우 하이퍼파라미터 튜닝이나, 다양한 모델 학습 스킬 등을 이용하여 최대한 전역 최솟값에 가깝게 도달하도록 해야 합니다.
- 로지스틱 회귀의 경우, 선형 회귀와 달리 MSE (Mean Squared Error) 손실 함수를 적용하게 되면 Non-Convex 해지게 됩니다. 따라서 학습이 제대로 진행되지 않거나, 최적화 과정에서 지역 최솟값(local minima)에 갇혀 전역 최솟값(global minimum)을 찾지 못할 수 있습니다. 따라서 로지스틱 회귀의 경우, MSE 손실 함수 대신에 Convex 한 BCE loss를 적용합니다.
- 자세한 내용은 아래 내용을 참고해 주시길 바랍니다.
- https://comdon-ai.tistory.com/22
- Convex 하지 않은 손실함수를 적용하게 되면 경사하강법을 적용할 때, 제대로 된 방향성을 찾지 못해 학습이 제대로 이루어지지 않게 될 수 있습니다.
회귀와 분류의 손실 함수 차이
- 회귀는 단순히 값의 차이를 최소화하는 방식으로 오차를 줄이지만, 분류는 확률적 접근을 통해서 불확실성을 최소화하면서 정확한 범주를 예측하려고 합니다.
- 회귀는 차이를 최소화 / 분류는 확률(0~1)을 최대화
- 회귀의 경우는 단순히 m개의 데이터셋에 대해서 하나의 데이터에 대한 loss 값을 더해서 평균을 내는 방식으로 진행하면 됩니다.
- 분류의 경우는 확률적인 개념이기때문에 각각의 데이터가 독립적으로 발생할 확률은 개별 확률의 곱으로 나타낼 수 있습니다. (=여러 개의 독립 사건들의 결합 확률을 구할 때 적용되는 것) 이 값을 최대화할 수 있는 loss 식을 만들어내야 합니다.(loss는 최소화하는 방향으로 진행해야 하기 때문에 -를 통해 방향을 바꿔줘야 합니다.)
- 정리하면 m개의 크기의 데이터셋이 주어졌을 때 이에 대한 비용 함수의 경우 회귀는 모두 더해서 평균을 내지만, 분류의 경우 모두 곱한 확률값을 최대화해야 합니다.
- 하지만 분류의 경우 위와 같이 곱할 경우 문제가 존재합니다.
- 첫 번째로 확률끼리 곱해지므로 특정한 확률값이 0에 가까워진다면 곱셈을 할 때 불안정해지는 문제가 있습니다.
- 두 번째로는 데이터셋의 길이에 따라 곱해지는 길이도 달라지기 때문에 데이터셋 규모에 따라 변하는 loss가 변하는 문제가 존재할 수 있습니다.
- 위와 같은 문제를 해결하기 위해서 다음과 같은 해결방법이 존재합니다.
- 곱셈을 할 때 불안정해지는 문제를 해결하기 위해 곱해진 확률 값에 log를 씌워주는 방법입니다. (log는 모든 양의 입력값에 대해 단조 증가함수이기 때문에 log를 붙여주더라도 방향성에 변화는 없습니다.)
- 분류는 확률의 개념이기 때문에 0~1 사이 값을 가지므로 양의 입력값을 가지게 됩니다.
- log를 붙여주게 되면 log(p(a)p(b)p(c)p(d)) = log(p(a)) + log((p(b)) + log((p(c)) + log((p(d)) 처럼 확률의 곱셈이 덧셈으로 변해 수치적인 안정석을 가지게 됩니다.
- 여기서 잠깐 생각해 볼 점이 log(0)의 경우 -무한대가 되기 때문에 문제가 발생할 수 있는데 이건 어떻게 처리해야 할까요?
- 이는 log 안에 매우 작은 상수 (epsilon)을 더하는 방법으로 해결해 줄 수 있습니다. (log(p+ ))
- 또는 loss function clipping(손실 함수 클리핑) 방법을 통해 확률 p가 0에 매우 가까울 때는 임곗값으로 대체하는 방법도 존재합니다.
- 또한 길이의 문제의 경우는 log를 통해 곱셈을 덧셈으로 변경했으므로 데이터 개수의 크기(m)만큼을 나눠주는 방법을 통해 해결이 가능합니다.
- 곱셈을 할 때 불안정해지는 문제를 해결하기 위해 곱해진 확률 값에 log를 씌워주는 방법입니다. (log는 모든 양의 입력값에 대해 단조 증가함수이기 때문에 log를 붙여주더라도 방향성에 변화는 없습니다.)
- 회귀의 경우 손실 함수를 만드는 것은 그냥 차이를 줄여주는 방향으로 진행하면 되기때문에 어렵지 않습니다. 하지만 분류의 경우 확률적으로 접근해야 하기 때문에 다소 헷갈릴 수가 있습니다. 로지스틱 회귀(이름은 회귀지만 분류)의 이진 분류 손실 함수인 BCE 손실 함수 유도 과정을 살펴본다면 보다 쉽게 이해가 될 수 있습니다.
- BCE 손실 함수 유도 과정 : https://comdon-ai.tistory.com/22
손실 함수가 Convex 한 지 확인하기
- 손실 함수가 매개변수에 대해 Convex 한지 Non-Convex 한지 알기 가장 쉬운 방법
- [일변수인 경우] (=매개변수가 1개)
- 함수의 이차 도함수가 모든 점에서 양수이면(
 ) 그 함수는 Strictly Convex 하다고 말합니다.
) 그 함수는 Strictly Convex 하다고 말합니다. - 함수의 이차 도함수가 모든 점에서 0 또는 양수이면(
 ) 그 함수는 Convex 하다고 말합니다.
) 그 함수는 Convex 하다고 말합니다.
- 함수의 이차 도함수가 모든 점에서 양수이면(
- [다변수인 경우]
- 함수의 Hessian 행렬이 모든 점에서 Positive Definite이면, (즉, 모든 비제로 벡터 v에 대해
 ) 그 함수는 Strictly Convex하다고 말합니다.
) 그 함수는 Strictly Convex하다고 말합니다. - 함수의 Hessian 행렬이 모든 점에서 Positive Semi-Definite이면, (즉, 모든 벡터 v에 대해
 ) 그 함수는 Convex하다고 합니다.
) 그 함수는 Convex하다고 합니다. - 다변수 함수 f(w1, w2, ..., wn)에 대한 Hessian 행렬
- 함수의 Hessian 행렬이 모든 점에서 Positive Definite이면, (즉, 모든 비제로 벡터 v에 대해
- [일변수인 경우] (=매개변수가 1개)
- 그렇다면 로지스틱 회귀에서 왜 MSE loss를 사용하지 않고, BCE loss를 사용하는지 살펴보도록 하겠습니다.
- 하지만 많은 딥러닝문제에서는 비볼록(non-convex) 손실 함수를 자주 사용하게 됩니다. 로지스틱 회귀에서 시그모이드로 인하여 선형회귀에서는 모든 매개변수에 Convex 했던 MSE loss를 사용하지 못하는 것처럼 심층 신경망에서도 비선형 활성화 함수와 복잡한 네트워크 구조로 인해 대부분의 손실 함수가 매개변수에 대해 Non-Convex해지게 됩니다.
- 그렇다면 손실함수는 어떤 조건을 가져야 하는 것일까요?
손실 함수(loss function) 설계 시 고려할 점
- 0 이상의 값
- 손실 함수는 모든 가능한 예측에 대해 0 또는 양의 값이어야 합니다.
- 손실이나 오차가 없는 이상적인 경우를 0으로 표현하고, 오차가 클수록 그 값이 증가하는 구조를 가지도록 해야 합니다.
- 미분 가능성
- 많은 최적화 기법들이 손실 함수의 기울기(미분값)를 사용하기 때문에, 손실 함수는 모든 매개변수에 대해 미분 가능해야 합니다. 이를 통해 경사 하강법과 같은 알고리즘을 사용하여 최적의 매개변수를 찾을 수 있습니다
- 오차의 크기 반영
- 손실 함수는 실제 값과 예측 값 사이의 오차를 정량적으로 측정해야 합니다.
- 즉, 모델이 잘못된 예측을 할 때 더 높은 손실 값을 부여하여, 모델이 더 정확한 예측을 하도록 유도해야 합니다.
- 따라서 이상적인 손실 함수는 최소한 모델의 출력에 대해서는 볼록한 성질을 갖는 것이 바람직합니다.(즉, loss식이 모든 매개변수에 대해서는 Non-Convex 하더라도 최소한 y_hat(output값)에 대해 Convex 해야 합니다.)
- 아래는 BCE loss가 매개변수에 대해 Convex 한 지는 몰라도(대부분의 딥러닝 모델에서는 모델의 매개변수에 대한 손실 함수의 표면이 대체로 비볼록(non-convex) 합니다.), y_hat(=모델의 output)에 대해서 Convex 하다는 것을 증명한 것입니다.
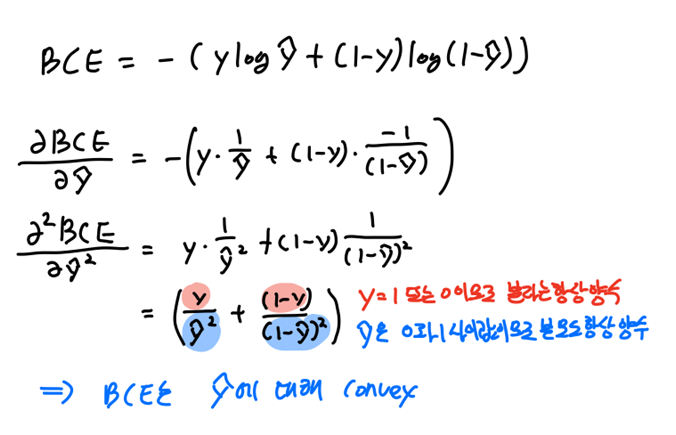
- 단, y_hat의 범위는 시그모이드를 통해 0~1 사이값이어야 합니다.
'AI > Basic' 카테고리의 다른 글
| 대표적인 Activation Function (Sigmoid, tanh, ReLU, Leaky ReLU, ELU, PReLU, Softplus, Swish) (0) | 2023.11.21 |
|---|---|
| 신경망 기초 (0) | 2023.11.10 |
| 경사 하강법(Gradient Descent) (1) | 2023.09.28 |
| 손실 함수(Loss function) vs 비용 함수(Cost function) (0) | 2023.09.28 |
| 로지스틱 회귀(Logistic Regression) (0) | 2023.09.28 |