목차
링크드 리스트(Linked List)
개념
- Linked List는 Node라는 구조체로 이루어져 있습니다.
- Node는 data와 인접한 Node의 주소(address)를 저장하고 있습니다.
- 하나의 Array는 data만 저장하기 때문에 각 공간의 크기는 4byte였습니다. 하지만 Linked List의 경우 주소까지 저장해 야하기 때문에 하나의 공간에는 8byte의 공간이 사용됩니다.
- 인접한 Node의 주소를 저장하기 때문에, Array처럼 기존 고정된 크기의 연속된 메모리 공간을 할당할 필요 없습니다. 데이터가 추가되는 시점에 메모리를 할당해 주면 됩니다.
- 불연속적(discontinuous)
- Node는 data와 인접한 Node의 주소(address)를 저장하고 있습니다.
- 링크드 리스트 종류
- Singly Linked List
- Doubly Linked List
- Singly Linked List
Singly Linked List
- Singly Linked List
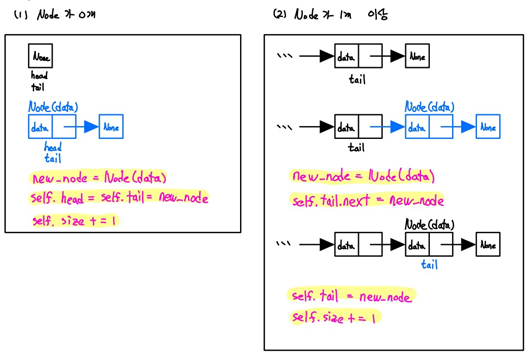
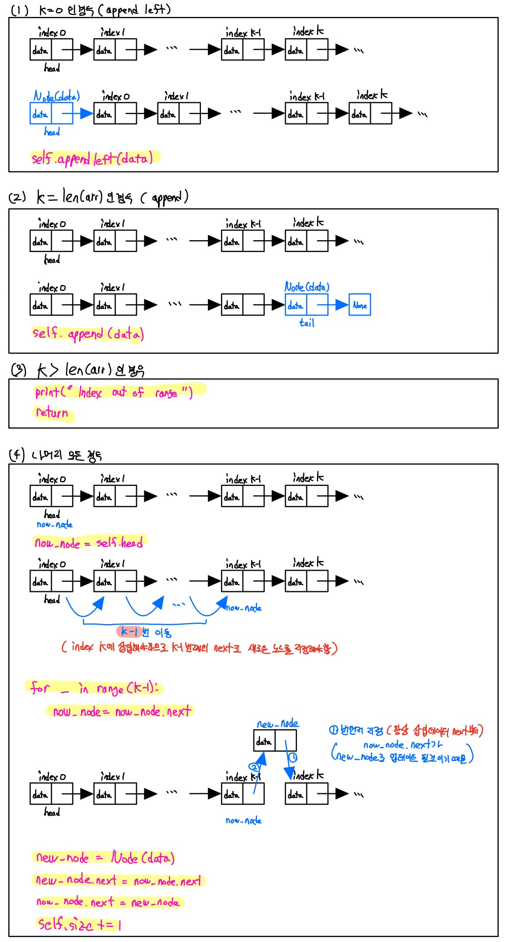
- append(data)
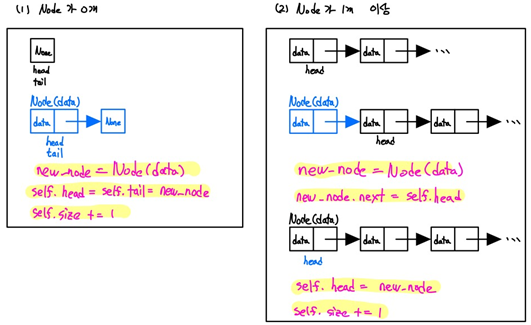
- appendleft(data)
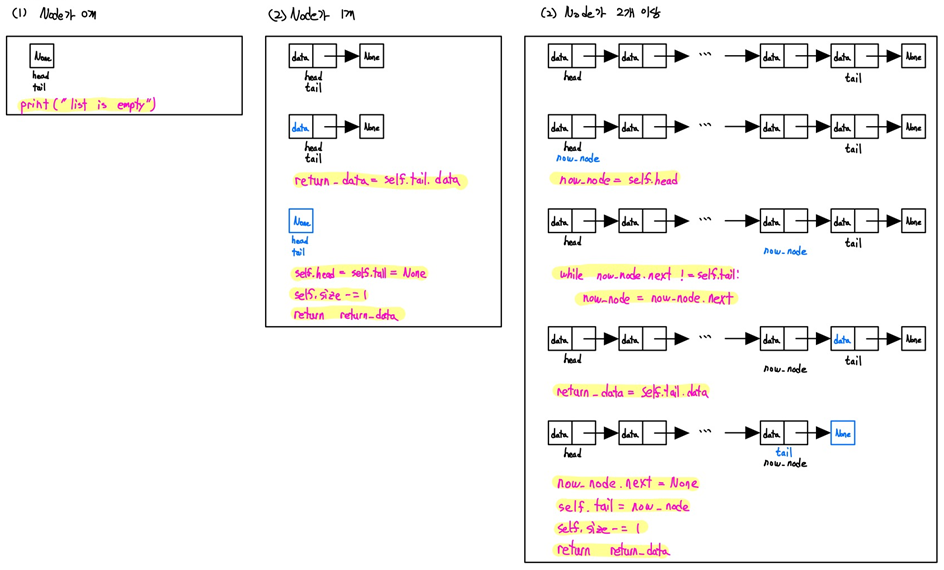
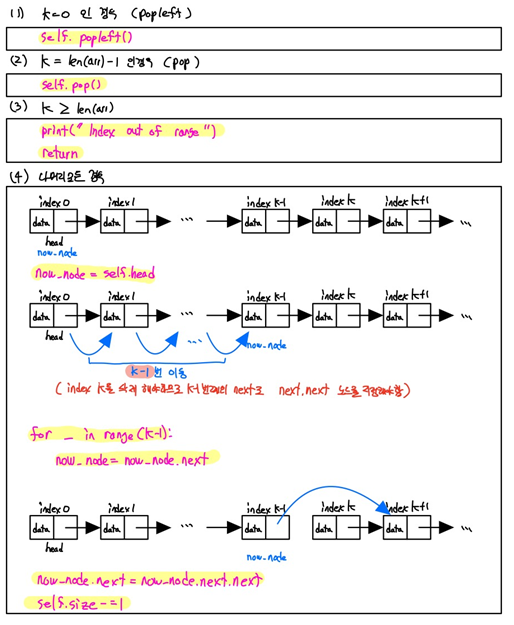
- pop()
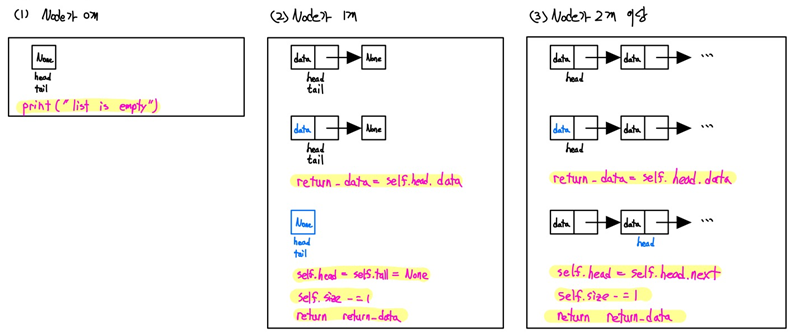
- popleft()
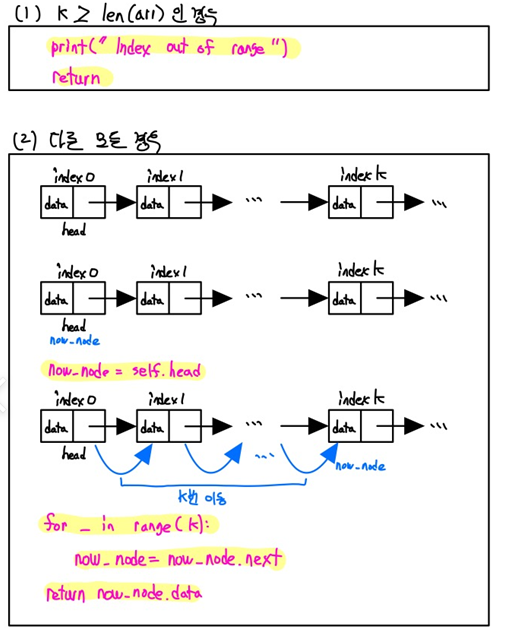
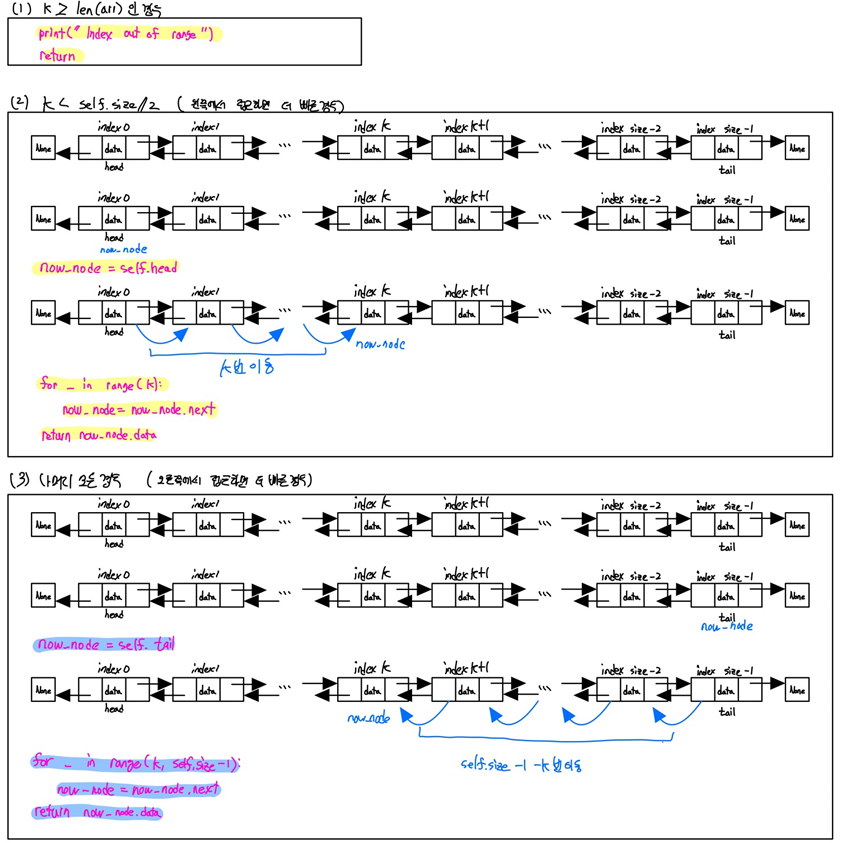
- find_index(index=k)
- insert_index(index=k, data)
- delete_index(index=k, data)
- 전체 코드
-
class Node: def __init__(self, data): self.data = data self.next = None class SinglyLinkedList: def __init__(self): self.head = None self.tail = None self.size = 0 def __len__(self): return self.size def append(self, data): if self.size == 0: new_node = Node(data) self.head = self.tail = new_node self.size += 1 else: new_node = Node(data) self.tail.next = new_node self.tail = new_node self.size += 1 def appendleft(self, data): if self.size == 0: new_node = Node(data) self.head = self.tail = new_node self.size += 1 else: new_node = Node(data) new_node.next = self.head self.head = new_node self.size += 1 def pop(self): if self.size == 0: print("list is empty") elif self.size == 1: return_data = self.tail.data self.head = self.tail = None self.size -= 1 return return_data else: now_node = self.head while now_node.next != self.tail: now_node = now_node.next return_data = self.tail.data now_node.next = None self.tail = now_node self.size -= 1 return return_data def popleft(self): if self.size == 0: print("list is empty") elif self.size == 1: return_data = self.tail.data self.head = self.tail = None self.size -= 1 return return_data else: return_data = self.head.data self.head = self.head.next self.size -= 1 return return_data def find_index(self, index): if index >= self.size: print("Index Out of Range") else: now_node = self.head for _ in range(index): now_node = now_node.next return now_node.data def insert_index(self, index, data): if index == 0: self.appendleft(data) elif index == self.size: self.append(data) elif index > self.size: print("Index Out of Range") else: now_node = self.head for _ in range(index - 1): now_node = now_node.next new_node = Node(data) new_node.next = now_node.next now_node.next = new_node self.size += 1 def delete_index(self, index): if index == 0: self.popleft() elif index == self.size - 1: self.pop() elif index > self.size - 1: print("Index Out of Range") else: now_node = self.head for _ in range(index - 1): now_node = now_node.next now_node.next = now_node.next.next self.size -= 1 def print_list(self): now_node = self.head while now_node: print(now_node.data, end=" ") now_node = now_node.next print() SLL = SinglyLinkedList() for i in range(10): SLL.append(i) SLL.print_list() # 0 1 2 3 4 5 6 7 8 9 print(SLL.find_index(5)) SLL.delete_index(5) # 0 1 2 3 4 6 7 8 9 SLL.print_list() SLL.delete_index(20) # Index Out of Range SLL.print_list() SLL.pop() # 1 2 3 4 6 7 8 9 SLL.popleft() # 1 2 3 4 6 7 8 SLL.print_list() SLL.appendleft(20) # 20 1 2 3 4 6 7 8 SLL.appendleft(30) # 30 20 1 2 3 4 6 7 8 SLL.print_list() print(len(SLL)) # 9
-
- append(data)
Doubly Linked List
- Doubly Linked List
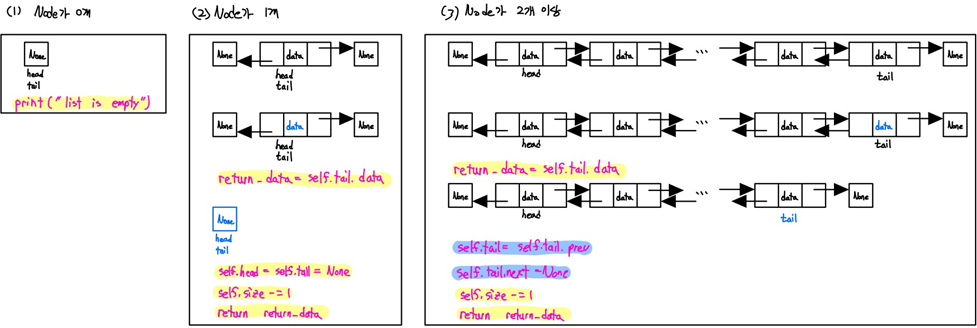
- Doubly Linked List 는 노드에서 prev가 추가된 것입니다. 따라서 뒤에서부터도 접근이 가능해집니다. Singly Linked List에서 prev가 추가된 것입니다.
- 뒤에서부터 접근이 가능하기 때문에 pop 코드가 단순화 되고, find_index, insert_index, delete_index 코드가 왼쪽과 오른쪽에서 접근이 가능해져 조금더 빠른 탐색이 가능해집니다.
- pop()
- find_index(index=k)
- insert_index와 delete_index도 find_index와 마찬가지로 동작합니다.
시간복잡도
- 링크드 리스트(Linked List)의 시간복잡도
- 특정 인덱스 값에 접근 : O(n)
- 시작 지점부터 해당 인덱스까지 주소를 타고 타고 가야지 확인이 가능합니다.
- Linked List 마지막에 data 추가 : O(1)
- 다음 data를 추가해 주고, 해당 주소를 기존 Linked List가 이어서 가르키면 됩니다.
- Linked List 마지막 data 삭제 : O(1)
- 단순하게 마지막 data를 삭제해 주면 됩니다.
- Linked List 중간에 data 삽입 : O(1)
- Array처럼 전체 배열을 움직일 필요 없이 address만 수정해 주면 됩니다.
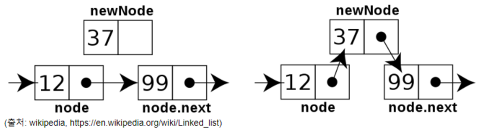
- Linked List 중간 data 삭제 : O(1)
- 삽입할 때와 마찬가지로 Array처럼 전체 배열을 움직일 필요 없이 address만 수정해 주면 됩니다.
- Linked List 특정 값 찾기 : O(n)
- Array처럼 하나하나 타고 들어가면서 해당 값이 있는지 확인해봐야 합니다.
- 주의할 점
- data를 삽입하고, 삭제하는 과정에서는 Linked List에서의 시간복잡도가 O(1)이지만, 실질적으로 해당 노드까지 찾아가는 과정이 O(n)이 걸리게 됩니다. 따라서 실질적인 시간복잡도는 O(n)입니다.
- 하지만 이제 만약 연속적으로 해당 부분에 데이터를 삽입하거나, 삭제할 때는 찾아가기만 하면 연속적으로 O(1)만으로 계속해서 처리가 가능합니다.
- 특정 인덱스 값에 접근 : O(n)
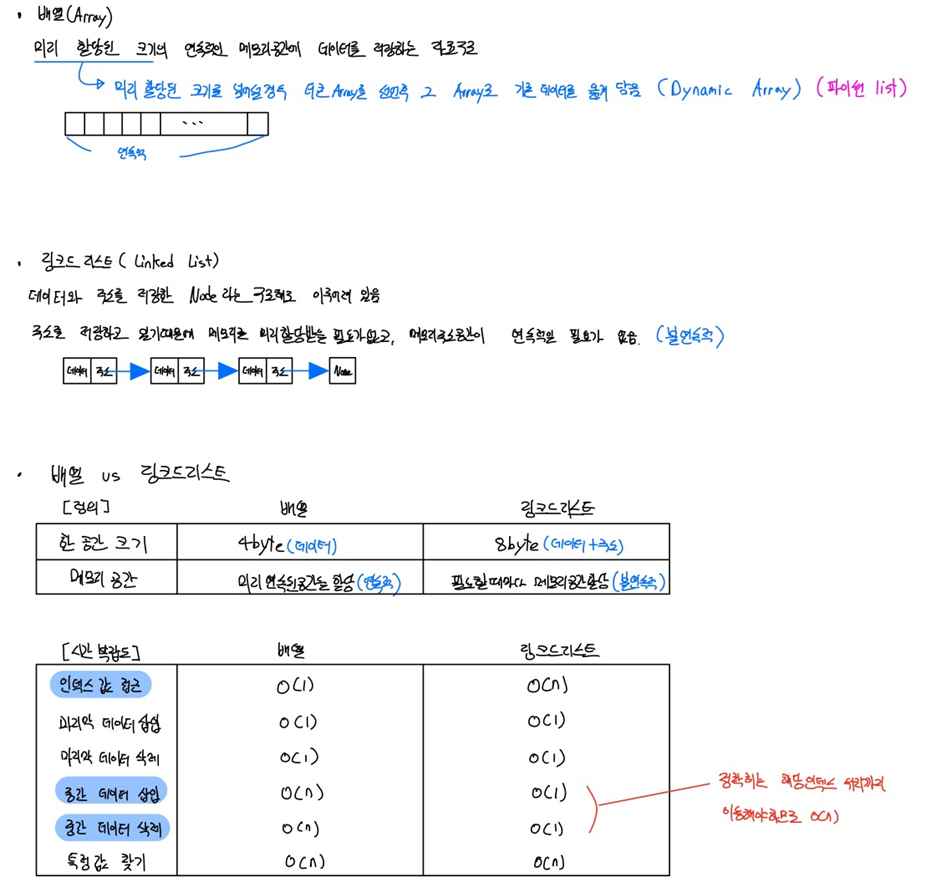
배열과 링크드리스트 차이
- 배열과 링크드리스트 차이
- 배열
- 연속되고 고정된 크기의 메모리에 데이터 할당
- 각 데이터 공간의 크기는 4byte
- 링크드리스트
- 연속적이지 않은 메모리 공간에 각 데이터들이 할당(비연속적) (주소를 통해 해당 데이터들 지정)
- 각 데이터 공간의 크기는 주소를 지정하여야 하므로 8byte
- 배열
배열과 시간복잡도 비교
- 배열과 시간복잡도 비교
- 특정 인덱스 값에 접근
- 배열(Array) : O(1)
- 링크드리스트(Linked List) : O(n)
- 마지막에 데이터 추가
- 배열(Array) : O(1)
- 링크드리스트(Linked List) : O(1)
- 마지막 데이터 삭제
- 배열(Array) : O(1)
- 링크드리스트(Linked List) : O(1)
- 중간에 데이터 삽입
- 배열(Array) : O(n)
- 링크드리스트(Linked List) : O(1)
- 중간에 데이터 삭제
- 배열(Array) : O(n)
- 링크드리스트(Linked List) : O(1)
- 특정값 찾기
- 배열(Array) : O(n)
- 링크드리스트(Linked List) : O(n)
- 특정 인덱스 값에 접근
'Computer Science > 자료구조(Data Structure)' 카테고리의 다른 글
| [자료구조] 삽입 정렬(Insertion Sort) (0) | 2024.04.16 |
|---|---|
| [자료구조] 버블 정렬(Bubble Sort) (0) | 2024.04.16 |
| [자료구조] 선택 정렬(Selection Sort) (0) | 2024.04.15 |
| [자료구조] 배열(Array) (0) | 2024.04.15 |
| 팬케이크 정렬(Pancake sort) (0) | 2024.03.15 |