목차
배열(Array)
개념
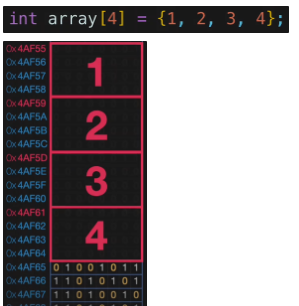
- Array는 미리 할당된 크기의 메모리에 연속적으로 data를 저장하는 자료구조입니다.
- C언어에서 배열의 각 크기는 4byte입니다.
- Array는 미리 할당된 크기에 data를 저장하는 한계점이 존재합니다. → 이는 Dynamic Array를 통해 보완가능합니다.
- 만약 미리 할당된 크기를 넘어설 경우, 더 큰 Array를 선언하고 그 Array에 기존 데이터를 옮겨 담습니다.
- 더 큰 Array의 size는 일반적으로 기존 Array size의 2배를 할당합니다. (doubling 방법)
- 데이터를 옮겨 담을 때는 O(n) 시간이 걸립니다.
- 즉, 기본적으로 제일 뒤에 데이터를 추가할 때는 O(1)이지만, 만약 기존 크기를 넘어서는 순간 제일 뒤에 데이터를 추가하게 되면 새로운 Array를 선언하고, 해당 Array로 기존 데이터를 옮기는 작업으로 인해 해당 순간에는 O(n)이 걸리게 됩니다. 옮긴 후 다시 제일 뒤에 데이터를 추가할 때는 다시 기존처럼 O(1)만에 데이터 추가가 가능합니다.
- 파이썬은 Dynamic array인 List를 사용합니다.
-
import sys data = [] print("--- append 시작 ---") for k in range(20): a = len(data) b = sys.getsizeof(data) print("Length: {0:3d}; Size in bytes : {1:4d}".format(a, b)) data.append(k) print("--- pop 시작 ---") for _ in range(20): data.pop() a = len(data) b = sys.getsizeof(data) print("Length: {0:3d}; Size in bytes : {1:4d}".format(a, b)) -
더보기--- append 시작 ---
Length: 0; Size in bytes : 56
Length: 1; Size in bytes : 88
Length: 2; Size in bytes : 88
Length: 3; Size in bytes : 88
Length: 4; Size in bytes : 88
Length: 5; Size in bytes : 120
Length: 6; Size in bytes : 120
Length: 7; Size in bytes : 120
Length: 8; Size in bytes : 120
Length: 9; Size in bytes : 184
Length: 10; Size in bytes : 184
Length: 11; Size in bytes : 184
Length: 12; Size in bytes : 184
Length: 13; Size in bytes : 184
Length: 14; Size in bytes : 184
Length: 15; Size in bytes : 184
Length: 16; Size in bytes : 184
Length: 17; Size in bytes : 248
Length: 18; Size in bytes : 248
Length: 19; Size in bytes : 248
--- pop 시작 ---
Length: 19; Size in bytes : 248
Length: 18; Size in bytes : 248
Length: 17; Size in bytes : 248
Length: 16; Size in bytes : 248
Length: 15; Size in bytes : 248
Length: 14; Size in bytes : 248
Length: 13; Size in bytes : 248
Length: 12; Size in bytes : 248
Length: 11; Size in bytes : 184
Length: 10; Size in bytes : 184
Length: 9; Size in bytes : 184
Length: 8; Size in bytes : 184
Length: 7; Size in bytes : 152
Length: 6; Size in bytes : 152
Length: 5; Size in bytes : 120
Length: 4; Size in bytes : 120
Length: 3; Size in bytes : 120
Length: 2; Size in bytes : 120
Length: 1; Size in bytes : 88
Length: 0; Size in bytes : 56
-
시간복잡도
- Array의 시간복잡도
- 특정 인덱스 값에 접근 : O(1)
- 연속된 메모리이기때문에 인덱스 값만 알면 바로 접근이 가능합니다.
- Array 마지막에 data 추가 : O(1)
- 연속된 메모리이기때문에 그냥 그 뒤에 데이터를 바로 추가해 주면 됩니다.
- 참고 : 기존 Array 크기를 넘어서는 순간 데이터를 추가하게 되면 그 순간에는 O(n)이 걸리게 됩니다. (새로운 Array 선언 후 해당 Array로 데이터를 옮기는 시간으로 인하여 O(n) 소요)
- Array 마지막 data 삭제 : O(1)
- 연속된 메모리이기때문에 마지막에 있는 데이터를 단순하게 삭제하면 됩니다.
- Array 중간에 data 삽입 : O(n)
- 기존 연속된 메모리에서 중간에 비어있는 공간을 만들어주기 위해 삽입하고 싶은 부분의 뒷부분을 모두 한 칸씩 뒤로 옮겨주어야 합니다. 따라서 O(n)의 시간복잡도를 가집니다.
- Array 중간에 data 삭제: O(n)
- 기존 연속된 메모리에서 중간에 있는 값을 삭제하면 비어있는 공간이 생기는데, 그 부분을 메우기 위해 뒷 부분을 모두 한 칸씩 앞으로 옮겨주어야 합니다. 따라서 O(n)의 시간복잡도를 가집니다.
- 특정값 찾기 : O(n)
- 전체 연속된 메모리 공간을 하나씩 탐색하며 특정값이 있는지 체크를 진행해야합니다. 따라서 O(n)의 시간복잡도가 걸립니다.
- 특정 인덱스 값에 접근 : O(1)
'Computer Science > 자료구조(Data Structure)' 카테고리의 다른 글
| [자료구조] 삽입 정렬(Insertion Sort) (0) | 2024.04.16 |
|---|---|
| [자료구조] 버블 정렬(Bubble Sort) (0) | 2024.04.16 |
| [자료구조] 선택 정렬(Selection Sort) (0) | 2024.04.15 |
| [자료구조] 링크드 리스트(Linked List) (0) | 2024.04.15 |
| 팬케이크 정렬(Pancake sort) (0) | 2024.03.15 |



