목차
위상 정렬(Topological Sort)
- 위상 정렬(Topological Sort)은 방향 그래프의 모든 노드를 "방향성을 거스르지 않도록 순서대로 나열하는 것"을 말합니다.
- 즉, 그래프 상에서 어떤 노드로 가기 위한 선행 노드들을 모두 거친 후에 해당 노드를 방문할 수 있는 순서로 노드들을 나열하는 과정입니다.
- 위상 정렬은 일반적으로 사이클이 없는 방향 그래프(Directed Acyclic Graph, DAG)에서만 수행할 수 있습니다.
- 예를 들면, 수강신청을 할 때 선수과목이 있는 경우 선수 과목을 먼저 듣고 나서 해당 강의를 수강할 수 있습니다.
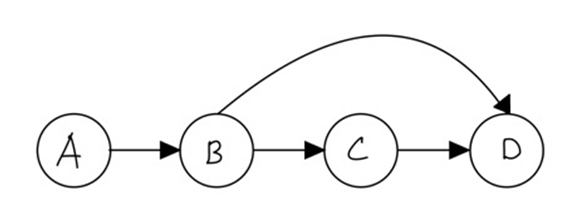
- A->B / B->C / B->D / C->D 가 있다고 할때, A, B, C, D 순서대로 들어야지 모든 과목을 수강할 수 있습니다.
- 만약 A B D C 라고 한다면, D의 경우 C를 듣지 않으면 수강할 수 없기 때문에 올바르지 않은 경우입니다.
- 즉 A B C D처럼 정렬된 경우를 위상정렬이 된 상태라고 할 수 있습니다.
- 위상 정렬이 필요한 경우는 그래프에서 반드시 자신보다 선행되어야 할 일을 다 끝내야만 작업에 들어갈 수 있는 조건이 주어질 때입니다.
- ex. 선수과목을 들어야지 다음 과목을 수강 가능
- 위상정렬
- (위상정렬은 사이클이 없을 경우에만 가능합니다. 만약 진행 과정 중에 방문했던 노드를 재방문하면 그것은 사이클이 존재하는 경우이기 때문에 위상정렬이 불가능합니다.)
- 사이클 여부는 최종 result에 들어가 있는 노드의 길이가 n보다 짧을 경우, 사이클이 있는 것입니다.
- 사이클이 있으면 indegree가 0인 노드가 없을 것입니다. 그렇기 때문에 중간에 사이클이 있는 부분에 들어가게 되면 q에 더 이상 노드가 들어가지 않습니다. 따라서 n개의 노드를 방문하기 전에 조기 종료할 것입니다.
- 1. 들어오는 간선이 없는 정점(진입차수가 0)을 큐에 모두 넣기
- 2. 해당 원소와 연결된 노드들을 진입차수에서 1 빼기
- 2-1. 1을 뺐을때 진입차수가 0이라면 큐에 넣어주기
- 3. 반복
- (위상정렬은 사이클이 없을 경우에만 가능합니다. 만약 진행 과정 중에 방문했던 노드를 재방문하면 그것은 사이클이 존재하는 경우이기 때문에 위상정렬이 불가능합니다.)
- 예시코드
-
from collections import deque # 그래프 설정. 노드와 간선의 수를 설정해주세요. n, m = map(int, input().split()) graph = [[] for i in range(n + 1)] indegree = [0] * (n + 1) # 간선 정보 입력받기 for _ in range(m): a, b = map(int, input().split()) graph[a].append(b) indegree[b] += 1 # 위상 정렬 함수 def topology_sort(): result = [] q = deque() # 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입 for i in range(1, n + 1): if indegree[i] == 0: q.append(i) # 큐가 빌 때까지 반복 while q: now = q.popleft() result.append(now) # 해당 원소와 연결된 노드들의 진입차수에서 1 빼기 for i in graph[now]: indegree[i] -= 1 # 새롭게 진입차수가 0이 되는 노드를 큐에 삽입 if indegree[i] == 0: q.append(i) # 위상 정렬 결과 출력 for i in result: print(i, end=' ') topology_sort()
-
예시
- [백준 2623] 음악프로그램
- 보조 PD들이 만든 순서를 보고, 전체 가수의 순서를 정해야 합니다.
- 즉, 방향그래프에서 간선들을 보고, 순서를 만족하는 전체 가수의 순서를 정하는 문제입니다.
- 위상정렬 문제
- 만약, 중간에 사이클이 존재한다면, 전체 가수의 순서를 결정할 수 없습니다.
- 코드
-
import sys from collections import deque input = sys.stdin.readline n, m = map(int, input().split()) graph = [[] for _ in range(n + 1)] indegree = [0 for _ in range(n + 1)] for _ in range(m): n_arr, *arr = list(map(int, input().split())) for i in range(len(arr) - 1): graph[arr[i]].append(arr[i + 1]) indegree[arr[i + 1]] += 1 q = deque() for i in range(1, n + 1): if indegree[i] == 0: q.append(i) answer = [] while q: now_node = q.popleft() answer.append(now_node) for next_node in graph[now_node]: indegree[next_node] -= 1 if indegree[next_node] == 0: q.append(next_node) if len(answer) < n: answer = [0] for i in range(len(answer)): print(answer[i])
-
- 보조 PD들이 만든 순서를 보고, 전체 가수의 순서를 정해야 합니다.
'Algorithm > Concepts' 카테고리의 다른 글
| 비트마스킹(Bit Masking) (0) | 2024.03.21 |
|---|---|
| 느리게 갱신되는 세그먼트 트리(Lazy Segment Tree) (0) | 2024.03.20 |
| 구간 트리(Segment Tree) (0) | 2024.03.20 |
| 최소 스패닝 트리(Minimum Spanning Tree, MST) (0) | 2024.03.20 |
| Union-Find (0) | 2024.03.20 |



