느리게 갱신되는 세그먼트 트리(Lazy Segment Tree)

느리게 갱신되는 구간 트리(Lazy Segment Tree)

세그먼트 트리랑 개념은 동일하지만, Lazy 세그먼트 트리는 특장 인덱스 값 하나만 update하는 것이 아닌, 구간의 값을 한 번에 update 해주는 경우에 사용합니다.
해당 구간을 업데이트할때 바로 업데이트를 진행하는 것이 아닌, lazy에 값을 저장해두었다가, 나중에 해당 노드로 들어가게 된다면, 거기에서 그 노드를 업데이트를 진행시켜줍니다.
- 세그먼트 트리의 경우 update 할때마다 해당구간에 대해서 업데이트를 진행해주게 되면, 그 구간에 대한 인덱스들을 모두 업데이트를 진행해야하기때문에 시간이 오래 걸리게 됩니다. 리스트 길이가 N개고 쿼리가 Q개라고 한다면 결국 쿼리 한개당 구간에 대한 인덱스를 모두 업데이트를 진행해야하기때문에 Nlog(N)만큼 시간이 걸립니다.
- 여기서 만약 lazy 세그먼트 트리를 사용할 경우, 우선 log(N)만큼으로 find할때처럼 값을 업데이트 해주고 나중에 필요하거나, 해당 값위치의 노드로 방문할 시에 lazy에 저장된 값이 있으면 그 값으로 업데이트를 진행시켜줍니다.
그림을 통한 이해
- 1,2,3,4,5 의 배열에 대해서 lazy segment tree 과정을 살펴보겠습니다. find의 과정은 동일하지만, update 과정이 달라질 것입니다.
- 먼저 세그먼트 트리 그림을 살펴보겠습니다.
- 여기서 만약 2~4번째 값을 3씩 더해주라는 쿼리문이 들어오면 어떤식으로 update가 진행될까요?
  - 기존 segment tree 같은 경우 segment tree의 해당 인덱스 지점의 리프 노드부터 부모노드까지 지속적으로 업데이트를 할것입니다. (즉 , 2번째 값 위치의 리프노드부터 부모노드까지 업데이트, 3번째 값 위치의 리프노드부터 부모노드까지 업데이트, 4번째 값 위치의 리프노드부터 부모노드까지 업데이트를 진행할 것입니다.)
    - 즉, segment tree는 리프노드 -> 부모노드로 값을 업데이트
    - lazy segment tree는 부모노드 부터 값을 업데이트. (segment tree의 find 처럼 접근.)
  - 이럴경우, 비효율적인 연산이 됩니다. 따라서 lazy segment tree의 경우 다음과 같이 필요한 지점만 우선적으로 업데이트를 진행해줍니다.
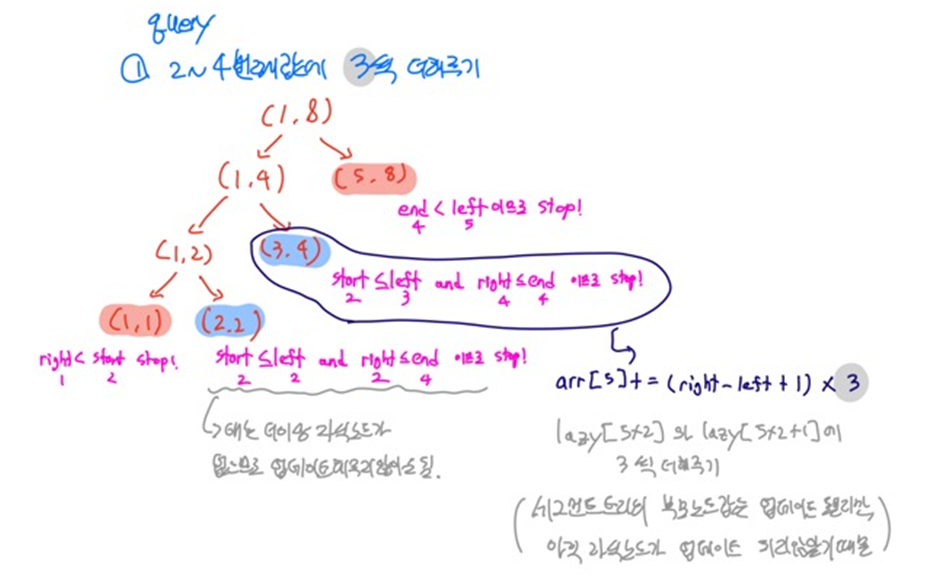
    - 세그먼트 트리 전체가 모두 업데이트 되지 않은것을 확인할 수 있습니다. arr[5]는 업데이트 됐지만, 그의 자식 노드인 arr[10]과 arr[11]은 업데이트 되지 않았습니다.
    - 이 값을 lazy[10] , lazy[11]에 넣어두고 추후에 해당 인덱스 노드에 방문할 경우, 그 lazy 값을 꺼내서 해당 인덱스의 세그먼트트리값을 업데이트 시켜줍니다.
      - 여기서 업데이트 시켜줄때 항상 중요한 점은, lazy[10]을 업데이트 시켰으면 lazy[20] lazy[21]인 자식 노드에 lazy[10]값을 그대로 등록을 시켜주어야합니다. (여기서는 20 21 인덱스가 없지만 설명을 위해 작성해주었습니다.)
      - 나중에 그 자식 노드도 방문했을때 해당 값으로 업데이트를 시켜주어야 하기때문입니다.
  - lazy에 있는 값은 update나 find 시에 해당 인덱스에 방문할때마다 lazy_update와 같은 함수를 통해 매번 해당인덱스에 lazy 값이 존재하는지 확인을 해주어야합니다.
    - lazy에 있는 값을 업데이트 해줄때는 해당 인덱스가 포함하는 범위, 즉 (right-left+1) 에 해당 lazy값을 곱한만큼을 업데이트 시켜주어야합니다. (구간합을 의미하기 때문입니다.)
    - 해당 lazy 값을 업데이트 시켜주었으면, 그의 자식노드에 해당 lazy 값을 전달해주어야합니다. 나중에 해당 자식 노드를 방문할때 업데이트를 시켜주기 위함입니다.
    - 참고 : 하지만 만약 구간합이 아닐경우는 다른 로직을 적용해 해당 lazy 값을 처리해주어야합니다.
예시 문제 [백준 10999] 구간합 구하기 2 를 통해 살펴보면 조금 더 수월하게 이해가 가능합니다.

예시

N개의 배열에서 연속되는 구간의 값을 변경하고, 연속되는 구간의 합을 구하는 문제입니다.
- 연속되는 구간의 연산을 구하기 때문에 segment tree로 접근해야 합니다. (segment tree를 사용하지 않을 경우 매번 슬라이싱 해서 하나의 쿼리마다 O(N)의 시간이 소요될 것입니다. segment tree를 사용하면 그대로 세그먼트 트리를 탐색해서 저장한 값을 불러오면 됩니다. O(log(N) 시간 소요)
연속되는 구간의 값을 변경하기 때문에 lazy segment tree를 사용해야합니다. (하나의 값만 업데이트 할 경우는 단순하게 segment tree를 사용해도 됩니다.)
- 연속되는 구간의 값을 하나씩 변경한다고 하면은 log(N)이 연속된 구간의 길이만큼 반복될것입니다. -> 비효율적
- 연속되는 구간의 합을 find 하는 것처럼 업데이트를 진행합니다. (대신 접근하지 못한 자식 노드들은 lazy를 통해 기록해두고, 추후에 해당 노드에 방문하면, 해당 lazy값을 이용해 해당 노드의 값을 업데이트 해줍니다.)

코드

import sys
import math

input = sys.stdin.readline

n, m, k = map(int, input().split())

max_n = 2 ** (math.ceil(math.log2(n)))

seg_tree = [0 for _ in range(max_n * 2)]


def init_update(idx, value):  # segment tree의 update함수와 동일
    idx = max_n + idx
    seg_tree[idx] = value
    while idx > 1:
        idx = idx // 2
        seg_tree[idx] = seg_tree[idx * 2] + seg_tree[idx * 2 + 1]


for i in range(n):
    init_update(i, int(input()))

lazy_tree = [0 for _ in range(max_n * 2)]


def update_lazy(idx, left, right):
    if lazy_tree[idx] != 0:
        seg_tree[idx] += (right - left + 1) * lazy_tree[idx]
        if left != right:  # 자식노드가 있는 경우
            lazy_tree[idx * 2] += lazy_tree[idx]
            lazy_tree[idx * 2 + 1] += lazy_tree[idx]
        lazy_tree[idx] = 0


def update(start, end, left, right, idx, value):
    # 항상 노드에 접근할때마다 lazy_tree에 업데이트 할 값이 있는지 체크하기
    update_lazy(idx, left, right)
    if left > end or right < start:
        return
    elif start <= left and right <= end:
        seg_tree[idx] += (right - left + 1) * value
        if left != right:  # 자식노드가 있는 경우
            lazy_tree[idx * 2] += value
            lazy_tree[idx * 2 + 1] += value
    else:
        mid = (left + right) // 2
        left = update(start, end, left, mid, idx * 2, value)
        right = update(start, end, mid + 1, right, idx * 2 + 1, value)
        # 업데이트 완료후 해당 자식노드들을 가지고 부모노드 다시 업데이트 진행해주기
        seg_tree[idx] = seg_tree[idx * 2] + seg_tree[idx * 2 + 1]


def find(start, end, left, right, idx):
    update_lazy(idx, left, right)
    if left > end or right < start:
        return 0
    elif start <= left and right <= end:
        return seg_tree[idx]
    else:
        mid = (left + right) // 2
        left = find(start, end, left, mid, idx * 2)
        right = find(start, end, mid + 1, right, idx * 2 + 1)
        return left + right


for _ in range(m + k):
    a, *order = map(int, input().split())
    if a == 1:  # 구간에 값 더해주기
        b, c, d = order
        update(b - 1, c - 1, 0, max_n - 1, 1, d)
    elif a == 2:  # 구간합 출력하기
        b, c = order
        print(find(b - 1, c - 1, 0, max_n - 1, 1))

[백준 14245] XOR

XOR 은 비트 연산자에서 둘 중에 하나만 1일 경우 1을 반환합니다. (즉, 0 0 -> 0 / 1 1 -> 0 / 1 0 -> 1 / 0 1 -> 1)
따라서 같은값끼리 XOR 연산을 하면 0이 되고 0과 XOR연산을 할 경우 자기 자신이 나오게 됩니다.
이와 같은 논리를 통해서 lazy나 seg_tree 값을 업데이트할때 길이가 짝수이면, 0에 xor 연산자를 하는 것이기때문에 그대로 두고, 길이가 홀수 일경우에만 xor 연산을 해주면 됩니다.
- 똑같은 숫자를 짝수번 xor 연산하면 0, 홀수번 연산하면 원래 숫자 그대로

코드

import sys
import math

input = sys.stdin.readline

n = int(input())

max_n = 2 ** (math.ceil(math.log2(n)))

seg_tree = [0 for _ in range(2 * max_n)]

arr = map(int, input().split())


def init_update(idx, value):
    idx = max_n + idx
    seg_tree[idx] = seg_tree[idx] ^ value
    while idx > 1:
        idx = idx // 2
        seg_tree[idx] = seg_tree[idx * 2] ^ seg_tree[idx * 2 + 1]


for i, value in enumerate(arr):
    init_update(i, value)

lazy_tree = [0 for _ in range(2 * max_n)]


def lazy_update(idx, left, right):
    if lazy_tree[idx] != 0:
        if (right - left + 1) % 2 == 0:
            seg_tree[idx] = seg_tree[idx]
        else:
            seg_tree[idx] = seg_tree[idx] ^ lazy_tree[idx]
        if left != right:
            lazy_tree[idx * 2] = lazy_tree[idx * 2] ^ lazy_tree[idx]
            lazy_tree[idx * 2 + 1] = lazy_tree[idx * 2 + 1] ^ lazy_tree[idx]
        lazy_tree[idx] = 0


def update(start, end, left, right, idx, value):
    lazy_update(idx, left, right)
    if end < left or start > right:
        return
    elif start <= left and right <= end:
        if (right - left + 1) % 2 == 0:
            seg_tree[idx] = seg_tree[idx]
        else:
            seg_tree[idx] = seg_tree[idx] ^ value
        if left != right:
            lazy_tree[idx * 2] = lazy_tree[idx * 2] ^ value
            lazy_tree[idx * 2 + 1] = lazy_tree[idx * 2 + 1] ^ value
    else:
        mid = (left + right) // 2
        update(start, end, left, mid, idx * 2, value)
        update(start, end, mid + 1, right, idx * 2 + 1, value)
        seg_tree[idx] = seg_tree[idx * 2] ^ seg_tree[idx * 2 + 1]


def find(start, end, left, right, idx):
    lazy_update(idx, left, right)
    if end < left or start > right:
        return 0
    elif start <= left and right <= end:
        return seg_tree[idx]
    else:
        mid = (left + right) // 2
        left = find(start, end, left, mid, idx * 2)
        right = find(start, end, mid + 1, right, idx * 2 + 1)
        return left ^ right


m = int(input())

for _ in range(m):
    t, *order = map(int, input().split())
    if t == 1:  # a,b,c를 입력받아 구간 [a,b]의 각 원소에 c를 xor 하기
        a, b, c = order
        update(a, b, 0, max_n - 1, 1, c)
    elif t == 2:  # a번째 원소 값 출력
        print(find(order[0], order[0], 0, max_n - 1, 1))

[백준 16975] 수열과 쿼리 21

연속된 구간에 특정값을 더해주기때문에 lazy segment tree를 생각할 수 있습니다.
모두 위 문제들하고 동일하게 해결하면 됩니다.

코드

import sys
import math

input = sys.stdin.readline

n = int(input())

arr = list(map(int, input().split()))

max_n = 2 ** (math.ceil(math.log2(n)))
seg_tree = [0 for _ in range(max_n * 2)]


def init_update(idx, value):
    idx = max_n + idx
    seg_tree[idx] = value
    while idx > 1:
        idx = idx // 2
        seg_tree[idx] = seg_tree[idx * 2] + seg_tree[idx * 2 + 1]


for i, v in enumerate(arr):
    init_update(i, v)

lazy_tree = [0 for _ in range(max_n * 2)]


def lazy_update(idx, left, right):
    if lazy_tree[idx] != 0:
        seg_tree[idx] += (right - left + 1) * lazy_tree[idx]
        if left != right:
            lazy_tree[idx * 2] += lazy_tree[idx]
            lazy_tree[idx * 2 + 1] += lazy_tree[idx]
        lazy_tree[idx] = 0


def update(start, end, left, right, idx, value):
    lazy_update(idx, left, right)
    if right < start or left > end:
        return
    elif start <= left and right <= end:
        seg_tree[idx] += (right - left + 1) * value
        if left != right:
            lazy_tree[idx * 2] += value
            lazy_tree[idx * 2 + 1] += value
    else:
        mid = (left + right) // 2
        update(start, end, left, mid, idx * 2, value)
        update(start, end, mid + 1, right, idx * 2 + 1, value)
        seg_tree[idx] = seg_tree[idx * 2] + seg_tree[idx * 2 + 1]


def find(start, end, left, right, idx):
    lazy_update(idx, left, right)
    if right < start or left > end:
        return 0
    elif start <= left and right <= end:
        return seg_tree[idx]
    else:
        mid = (left + right) // 2
        l = find(start, end, left, mid, idx * 2)
        r = find(start, end, mid + 1, right, idx * 2 + 1)
        return l + r


m = int(input())

for _ in range(m):
    q, *order = map(int, input().split())

    if q == 1:
        a, b, c = order
        update(a - 1, b - 1, 0, max_n - 1, 1, c)
    elif q == 2:
        x = order[0]
        print(find(x - 1, x - 1, 0, max_n - 1, 1))

'Algorithm > Concepts' 카테고리의 다른 글

위상 정렬(Topological Sort) (0)	2024.03.21
비트마스킹(Bit Masking) (0)	2024.03.21
구간 트리(Segment Tree) (0)	2024.03.20
최소 스패닝 트리(Minimum Spanning Tree, MST) (0)	2024.03.20
Union-Find (0)	2024.03.20

컴돈AI

느리게 갱신되는 세그먼트 트리(Lazy Segment Tree)

느리게 갱신되는 구간 트리(Lazy Segment Tree)

예시

'Algorithm > Concepts' 카테고리의 다른 글

티스토리툴바

느리게 갱신되는 세그먼트 트리(Lazy Segment Tree)

느리게 갱신되는 구간 트리(Lazy Segment Tree)

예시

'Algorithm > Concepts' 카테고리의 다른 글

관련글

티스토리툴바