목차
이진 탐색 트리(BST:Binary Search Tree)
개념
- 이진 탐색 트리의 각 노드의 값은 왼쪽 서브트리에 있는 값들보다 커야 하고, 오른쪽 서브트리에 있는 값들보다는 작아야 합니다.
- 삽입

-
def insert(self, data): if self.root is None: self.root = Node(data) else: self._insert(self.root, data) def _insert(self, parent_node, data): if data < parent_node.data: if parent_node.left is None: parent_node.left = Node(data) else: self._insert(parent_node.left, data) else: if parent_node.right is None: parent_node.right = Node(data) else: self._insert(parent_node.right, data)
- 검색
- 목표 값이 노드 값과 같으면 노드를 반환합니다.
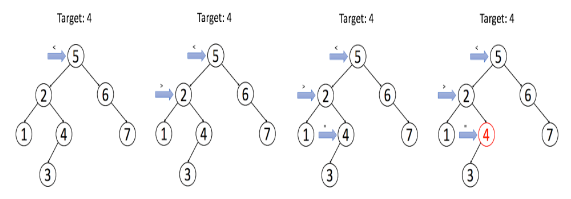
-
def search(self,data): return self._search(self.root,data) def _search(self, parent_node,data): if parent_node is None: return None elif parent_node.data == data: return parent_node elif parent_node.data < data: return self._search(parent_node.right,data) elif parent_node.data > data: return self._search(parent_node.left,data)
- 목표 값이 노드 값과 같으면 노드를 반환합니다.
- 삭제
- 만약 왼쪽 서브트리가 없으면 해당 오른쪽 서브트리의 루트 노드를 해당 자리로 옮겨주면 됩니다.
- 마찬가지로 오른쪽 서브트리가 없으면 해당 왼쪽 서브트리의 루트 노드를 해당 자리로 옮겨주면 됩니다.
- 위의 두경우는 이미 정렬이 되어 있는 경우이기 때문에 상관없지만 만약 왼쪽 서브트리와 오른쪽 서브트리가 모두 존재할 경우에는 오른쪽 서브트리 중에 제일 작은 값을 찾아서 삭제된 노드의 위치로 옮겨주어야 합니다.
- 해당 노드를 찾고 parent.data 에 해당 데이터를 옮기고 나면, 해당 값을 이제 해당 서브트레이서 delete를 다시 진행해주어야 합니다.
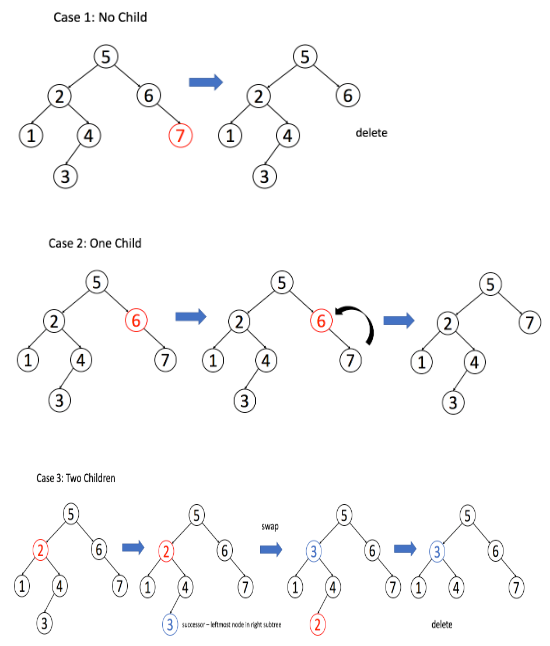
-
def delete(self,data): self.root = self._delete(self.root,data) def _delete(self, parent, data): if parent is None: return None elif data < parent.data: parent.left = self._delete(parent.left, data) elif data > parent.data: parent.right = self._delete(parent.right, data) elif data == parent.data: if parent.left is None: return parent.right elif parent.right is None: return parent.left else: temp = self._minvaluenode(parent.right) parent.data = temp.data parent.right = self._delete(parent.right,temp.data) # 옮겨온 노드 삭제 return parent # 해당 서브트리의 가장 작은 값까지 이동 def _minvaluenode(self,node): now_node = node while now_node.left: now_node = now_node.left return now_node
- 전체 코드
-
class Node: def __init__(self, data): self.data = data self.left = None self.right = None class BST: def __init__(self): self.root = None def insert(self, data): if self.root is None: self.root = Node(data) else: self._insert(self.root, data) def _insert(self, parent, data): if data < parent.data: if parent.left is None: parent.left = Node(data) else: self._insert(parent.left, data) else: if parent.right is None: parent.right = Node(data) else: self._insert(parent.right, data) def search(self,data): return self._search(self.root,data) def _search(self, parent, data): if parent is None: return None elif parent.data == data: return parent elif parent.data < data: return self._search(parent.right,data) elif parent.data > data: return self._search(parent.left,data) def delete(self,data): self.root = self._delete(self.root,data) def _delete(self, parent, data): if parent is None: return None elif data < parent.data: parent.left = self._delete(parent.left, data) elif data > parent.data: parent.right = self._delete(parent.right, data) elif data == parent.data: if parent.left is None: return parent.right elif parent.right is None: return parent.left else: temp = self._minvaluenode(parent.right) parent.data = temp.data parent.right = self._delete(parent.right,temp.data) # 옮겨온 노드 삭제 return parent # 해당 서브트리의 가장 작은 값까지 이동 def _minvaluenode(self,node): now_node = node while now_node.left: now_node = now_node.left return now_node
-
출처
'Computer Science > 자료구조(Data Structure)' 카테고리의 다른 글
| [자료구조] 힙(Heap) (1) | 2024.04.20 |
|---|---|
| [자료구조] 버킷 정렬(Bucket Sort) (0) | 2024.04.17 |
| [자료구조] 기수 정렬(Radix Sort) (0) | 2024.04.17 |
| [자료구조] 계수 정렬(Counting Sort) (0) | 2024.04.17 |
| [자료구조] 퀵 정렬(Quick Sort) (0) | 2024.04.17 |




