목차
정렬 종류
비교 기반 정렬(Comparison Based Sorts)
- Selection Sort, Bubble Sort, Insertion Sort, Heap Sort, Merge Sort, Quick Sort
비비교 기반 정렬(Non-comparison Based Sorts)
- Counting Sort, Radix Sort, Bucket Sort
병합 정렬(Merge Sort)
개념
- 병합 정렬은 분할 정복을 이용한 비교 기반 정렬입니다.
- 분할 정복은 일종의 DP랑 유사한 방법입니다. 따라서 분할 정복 역시 DP와 마찬가지로 하향식 접근(Top-Down)과 상향식(Bottom-Up) 접근이 존재합니다.
- 하향식 접근 : 재귀를 이용
- 상향식 접근 : 반복을 통해 모든 값 표 채우기
- 다만 DP는 분할 정복과 다르게 겹치는 하위 문제가 존재하는 경우 적용합니다.(분할 정복은 겹치는 하위 문제가 없습니다.)
- 분할정복에서의 하향식 접근은 단순히 재귀를 이용하지만(중간에 값을 저장할 필요가 없습니다.) DP에서는 겹치는 하위 문제가 존재하여 memoization기법이 추가로 적용됩니다. 즉, DP에서는 중간에 계산되는 결과를 저장해 재귀 과정에서 이미 저장된 값이 있다면 해당 값을 호출해서 반복연산을 줄여줄 수 있습니다.(Memoization)
- 분할정복에서의 상향식 접근은 중복되는 연산이 없기 때문에 이미 채워진 표의 값을 다시 이용하여 표를 채우지 않습니다. 하지만 DP에서는 겹치는 하위 문제가 존재하기 때문에 이미 채워진 표의 값을 이용하여 새로운 표의 값을 채워나갑니다.
- 분할 정복은 일종의 DP랑 유사한 방법입니다. 따라서 분할 정복 역시 DP와 마찬가지로 하향식 접근(Top-Down)과 상향식(Bottom-Up) 접근이 존재합니다.
- 병합 정렬은 매 단계마다 모든 원소에 대해서 체크를 진행하지만 단계수를 logN 만 체크를 진행하면 됩니다. 따라서 O(NlogN)만에 정렬이 가능해집니다. 공간 복잡도는 기존 배열들을 재배치하는 과정으로 인하여 새로운 공간을 생성해야해서 O(N)입니다.
- 하향식 접근

- 각 재귀 속 과정은 다음과 같습니다.

- 두 배열을 앞쪽부터 비교해 더 작은 값을 새로운 배열에 넣어줍니다. 이와 같은 과정을 계속 반복해서 진행하다가 한쪽 배열이 비게 될 경우, 나머지 한쪽 배열의 남은 값을 새로운 배열에 이어서 넣어줍니다.
- 상향식 접근
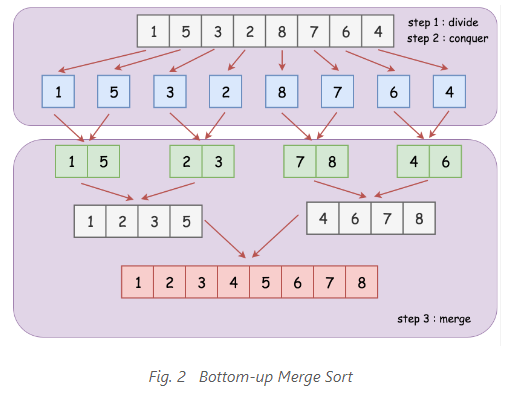
- 재귀가 아닌 단순하게 반복을 통해서 값을 채워주면 됩니다.
코드
- Merge Sort (Top-Down (하향식) )
-
def merge_sort(nums): if len(nums) <= 1: return nums pivot = len(nums) // 2 left_list = merge_sort(nums[:pivot]) right_list = merge_sort(nums[pivot:]) return merge(left_list, right_list) def merge(left_list, right_list): left_point = right_point = 0 merge_arr = [] while left_point < len(left_list) and right_point < len(right_list): if left_list[left_point] < right_list[right_point]: merge_arr.append(left_list[left_point]) left_point += 1 else: merge_arr.append(right_list[right_point]) right_point += 1 merge_arr.extend(left_list[left_point:]) merge_arr.extend(right_list[right_point:]) return merge_arr arr = [7, 3, 2, 5, 6, 10, 9, 8, 1] arr = merge_sort(arr) print(arr)
-
- Merge Sort (Bottom-Up (상향식) )
-
def merge_bu(arr, start, mid, end): left_list = arr[start:mid] right_list = arr[mid:end] left_point, right_point, idx = 0, 0, start while left_point < len(left_list) and right_point < len(right_list): if left_list[left_point] < right_list[right_point]: arr[idx] = left_list[left_point] left_point += 1 else: arr[idx] = right_list[right_point] right_point += 1 idx += 1 # 나머지 요소들을 복사하기 while left_point < len(left_list): arr[idx] = left_list[left_point] left_point += 1 idx += 1 while right_point < len(right_list): arr[idx] = right_list[right_point] right_point += 1 idx += 1 def merge_sort_bottom_up(arr): curr_size = 1 n = len(arr) while curr_size < n: for start in range(0, n, curr_size * 2): mid = min(start + curr_size, n) end = min(start + 2 * curr_size, n) merge_bu(arr, start, mid, end) curr_size *= 2 return arr arr = [7, 3, 2, 5, 6, 10, 9, 8, 1] arr = merge_sort_bottom_up(arr) print(arr)
-
출처
'Computer Science > 자료구조(Data Structure)' 카테고리의 다른 글
| [자료구조] 계수 정렬(Counting Sort) (0) | 2024.04.17 |
|---|---|
| [자료구조] 퀵 정렬(Quick Sort) (0) | 2024.04.17 |
| [자료구조] 힙 정렬(Heap Sort) (0) | 2024.04.16 |
| [자료구조] 삽입 정렬(Insertion Sort) (0) | 2024.04.16 |
| [자료구조] 버블 정렬(Bubble Sort) (0) | 2024.04.16 |



